- З проекту ВікіОсвіта Довжина хвилі де Бройля - довжина хвилі, яка проявляється у всіх частинок в...
- Висновок формули для довжини хвилі де Бройля
- Хвилі всередині частинок
- Електрони в атомах
- інші моделі
- посилання
З проекту ВікіОсвіта
Довжина хвилі де Бройля - довжина хвилі, яка проявляється у всіх частинок в квантовій механіці згідно корпускулярно-хвильовому дуалізму, і що визначає щільність ймовірності виявлення об'єкта в заданій точці конфігураційного простору. Довжина хвилі де Бройля обернено пропорційна імпульсу частки.
- 1 Визначення
- 2 Висновок формули для довжини хвилі де Бройля
- 2.1 У олни всередині частинок
- 2.2 Електрони в атомах
- 2.3 Інші моделі
- 3 Посилання
- 4 Зовнішні посилання
визначення
У 1924 році французький фізик Луї де Бройль припустив, що для частинок справедливі ті ж самі співвідношення, що і для фотона: [1]
де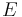 
і 
- енергія і імпульс фотона, 
і 
- частота і довжина хвилі фотона, 
- постійна Планка , 
- швидкість світла.
Звідси випливає визначення довжини хвилі де Бройля через постійну Планка і релятивістський імпульс частинки:
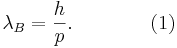
На відміну від фотонів, які завжди рухаються з однієї і тієї ж швидкістю, що дорівнює швидкості світла, у частинок згідно спеціальної теорії відносності імпульси залежать від маси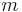 
і від швидкості руху 
за формулою
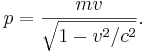
Висновок формули для довжини хвилі де Бройля
Існує кілька пояснень того, що в експериментах з частинками проявляється довжина хвилі де Бройля. Однак не всі ці пояснення можуть бути представлені в математичній формі, або вони не дають фізичного механізму, що обгрунтовує формулу (1).
Хвилі всередині частинок
При порушенні одних частинок іншими в ході експерименту, або при зіткненнях частинок з вимірювальними приладами, в частинках можуть виникати внутрішні стоячі хвилі. Це можуть бути електромагнітні хвилі або хвилі, пов'язані з сильним взаємодією частинок, з сильною гравітацією в гравітаційної моделі сильного взаємодії , і т.д. За допомогою перетворень Лоренца можна перерахувати довжину хвилі цих внутрішніх коливань в довжину хвилі, яку виявляє зовнішній спостерігач, який проводить експеримент з рухомими частинками. Розрахунок дає формулу для довжини хвилі де Бройля, [2] [3] [4] а також швидкість поширення хвилі де Бройля:
де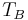 
- період коливань хвилі де Бройля.
Таким чином, виявляються основні риси, пов'язані з корпускулярно-хвильовим дуалізмом - якщо енергія внутрішніх стоячих хвиль в частинках досягає енергії спокою цих часток, то довжина хвилі де Бройля обчислюється так само, як у фотонів при відповідному імпульсі. Якщо ж енергія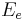 
збудження частинок менше енергії спокою 
, То довжина хвилі виходить за формулою:
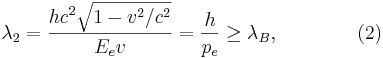
де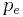 
- імпульс тієї маси-енергії, яка пов'язана з внутрішніми стоячими хвилями, і рухається разом з часткою зі швидкістю .
Очевидно, що в експериментах в основному проявляється довжина хвилі де Бройля (1), як гранична і найменша величина для довжини хвилі (2). У той же час експерименти з безліччю частинок можуть не дати однозначного значення для довжини хвилі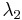 
за формулою (2) - якщо енергії збудження часток не контролюються і розрізняються у різних частинок, то розкид значень буде занадто великий. Чим вище енергії взаємодій і енергії збудження частинок, тим ближче вони будуть до енергії спокою і тим ближче буде довжина хвилі 
до 
. Легкі частки на зразок електронів швидше набувають швидкість порядку швидкості світла, стають релятивістськими і вже при малих енергіях демонструють квантові і хвильові властивості.
Крім довжини хвилі де Бройля, перетворення Лоренца дають ще одну довжину хвилі і її період:
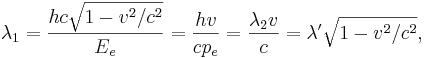
Ця довжина хвилі відчуває лоренцевское скорочення в порівнянні з довжиною хвилі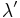 
в супутньої частці системі відліку. Крім цього, ця хвиля має швидкість свого поширення, рівну швидкості руху частинки. У граничному випадку, коли енергія збудження частинок дорівнює енергії спокою, 
, Для довжини хвилі маємо:
Отримана довжина хвилі є не що інше, як комптонівська довжина хвилі в ефекті Комптона, з поправкою на фактор Лоренца.
У представленій картині поява хвилі де Бройля і корпускулярно-хвильовий дуалізм трактуються як чисто релятивістський ефект, що виникає як наслідок лоренцевского перетворення стоячій хвилі, що рухається разом з часткою. При цьому, оскільки довжина хвилі де Бройля поводиться подібно довжині хвилі фотона з відповідним імпульсом, що об'єднує частки і хвилі, хвилі де Бройля вважаються хвилями ймовірності, пов'язаними з хвильової функцією. У квантовій механіці приймається, що квадрат амплітуди хвильової функції в даній точці в координатному представленні задає щільність ймовірності виявлення частки в цій точці.
У частинок електромагнітний потенціал спадає обернено пропорційно квадрату відстані від частки до точки спостереження, потенціал сильної взаємодії в гравітаційної моделі сильного взаємодії поводиться аналогічно. При виникненні внутрішніх коливань в частці коливається і потенціал поля навколо частинки, і отже, амплітуда хвилі де Бройля швидко росте при наближенні до частинки. Це як раз відповідає тому, що частка з більшою ймовірністю знаходиться там, де більше амплітуда її хвильової функції. Це вірно для чистого стану, наприклад, для однієї частинки. Якщо ж є змішане стан, коли в облік беруться хвильові функції декількох взаємодіючих частинок, трактування, що зв'язує хвильові функції і ймовірності стає не такою точною. В цьому випадку хвильова функція скоріше буде відображати амплітуду сумарною хвилі де Бройля, пов'язану з амплітудою сумарного хвильового поля потенціалів частинок.
Перетворення Лоренца для визначення довжини хвилі де Бройля були використані також в статті. [5]
Пояснення хвилі де Бройля через стоячі хвилі усередині частинок описується також в статті. [6] На відміну від цього, в статті [7] передбачається, що всередині частинки є кругова електромагнітна хвиля. Згідно з висновком в статті, [8] за межами рухається частинки повинна бути хвиля де Бройля з амплітудною модуляцією.
Електрони в атомах
Рух електронів в атомах відбувається шляхом їх обертання навколо атомних ядер. В субстанціональної моделі електрони являють собою хмари у формі дисків. Це є результатом дії чотирьох приблизно однакових за величиною сил, що виникають:
1) від тяжіння електрона до ядра за рахунок сильною гравітації і кулонівського тяжіння зарядів електрона і ядра, 2) від відштовхування зарядженого речовини електрона самого від себе, 3) від тікання речовини електрона від ядра за рахунок обертання, що враховується доцентровою силою.
В атомі водню електрон в стані з мінімальною енергією може бути моделирован обертовим диском, внутрішній край якого має радіус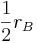 
, А зовнішній край - радіус 
, де 
є борівський радіус. [3]
Якщо припустити, що на орбіті електрона в атомі укладається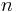 
довжин хвиль де Бройля, то при круговій орбіті з радіусом 
для довжини кола і моменту імпульсу електрона 
буде наступне:
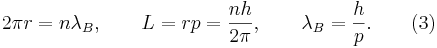
Це відповідає постулату Борівської моделі атома, за яким момент імпульсу в атомі водню квантів і пропорційний номером орбіти 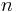і постійної Планка.
Однак енергія збуджень в речовині електронів в атомах на стаціонарних орбітах як правило не дорівнює енергії спокою самих електронів, і тому просторове квантування хвилі де Бройля уздовж орбіти в формі (3) слід пояснювати іншим способом. Зокрема було показано, що на стаціонарних орбітах в распредёлённом по простору речовині електрона здійснюється рівність потоку кінетичної енергії речовини і суми потоків енергії від електромагнітного поля і поля сильної гравітації. [3]
В цьому випадку потоки енергії полів не гальмують і не розкручують речовина електрона. Це дає рівноважні кругові і еліптичні орбіти електрона в атомі. При цьому виявляється, що моменти імпульсу квантуються пропорційно постійної Планка, що в першому наближенні приводить до співвідношення (3).
Крім цього, при переходах з однієї орбіти на іншу, ближчу до ядра, електрони випромінюють фотони, які забирають з атома енергію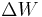 
і момент імпульсу 
. Для фотона корпускулярно-хвильовий дуалізм зводиться до прямого зв'язку між цими величинами, а їхнє ставлення 
дорівнює середній кутовий частоті хвилі фотона і одночасно середньої кутової швидкості електрона 
, Що випромінює при відповідних умовах фотон в атомі при своєму обертанні. Якщо вважати, що у кожного фотона 
, де 
є постійна Дірака , То тоді для енергії фотона маємо: 
. У такому випадку при атомних переходах момент імпульсу електрона також змінюється на , І повинна бути справедлива формула (3) для квантування моменту імпульсу в атомі водню.
При переході електрона з одного стаціонарного стану в інший в його речовині змінюються кільцевої потік кінетичної енергії і внутрішні потоки полів, а також їх імпульси і енергії. Синхронно з цим змінюється енергія електрона в полі ядра, випромінюється енергія фотона, збільшується імпульс електрона і зменшується довжина хвилі де Бройля в (3). Таким чином, випромінювання фотона як кванта електромагнітного поля з атома супроводжується зміною енергії потоків поля в речовині електрона, обидва процеси пов'язані з енергіями полів і зі зміною моменту імпульсу електрона, пропорційного .
Зі співвідношення (3) здається, що на електронній орбіті можна розташувати 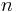довжин хвиль де Бройля. Але при цьому енергія збудження електрона не досягає енергії його спокою, як це потрібно для опису довжини хвилі де Бройля при поступальному русі частинок. Замість цього виникає зв'язок між моментами імпульсу і потоками енергії в речовині електрона в стаціонарних станах, і зв'язок при зміні цих моментів імпульсу і потоків при випромінюванні фотонів.
інші моделі
посилання
1. L. de Broglie, Recherches sur la théorie des quanta (Researches on the quantum theory), Thesis (Paris), 1924; L. de Broglie, Ann. Phys. (Paris) 3, 22 (1925).
2. Федосін С.Г. Фізика і філософія подібності від преонов до метагалактик , Перм: Стиль-МГ, 1999, 544 стор., Табл.66, Іл.93, Бібл. 377 назв. ISBN 5-8131-0012-1.
3. Федосін С. Г. Фізичні теорії і нескінченна вкладеність матерії , Перм, 2009 844 стр., Табл. 21, Іл.41, Бібл. 289 назв. ISBN 978-5-9901951-1-0.
4. Fedosin SG The radius of the proton in the self-consistent model . Hadronic Journal, 2012 Vol. 35, No. 4, P. 349 - 363; стаття російською мовою: Радіус протона в самосогласованной моделі .
5. Masanori Sato and Hiroki Sato. Interpretation of De Broglie Waves: At What Time Does a Massive Particle Obtain the Properties of a Wave? Physics Essays. 2012 Vol. 25, P. 150-156.
6. JX Zheng -Johansson and Per- Ivar Johansson. Developing de Broglie Wave . Progress in physics, 2006, Vol. 4, P.32-35.
7. Malik Mohammad Asif. de Broglie wave and electromagnetic travelling wave model of electron and other charged particles . Physics Essays. 2014 року, Vol. 27, P. 146-164.
8. J. Domínguez -Montes and EL Eisman, Representative model of particle-wave duality and entanglement based on De Broglie's interpretation . Physics Essays 2012 Vol. 25, P. 215-220.
