Деякий час тому кільком десяткам науковців з різних країн світу запропонували скласти список видатних діячів науки відповідно до того значенням, яке мало їх творчість для нашої цивілізації. Перші три місця одноголосно були віддані Архімеда, І. Ньютону і Ч. Дарвіном.

АРХИМЕД
Хто ж була ця людина, названий першим, і що він зробив, якщо вся світова спільнота одностайно визнало його самим великим ученим всіх часів і народів?
Біографічні відомості про Архімеда - давньогрецькому математики, фізики, астронома і інженера - украй мізерні. Відомо, що він був сином астронома і математика Фідія. Навчався і деякий час працював в Олександрії (Єгипет). Архімеда все життя пов'язували дружні стосунки з тамтешніми науковцями (Ератосфеном, Кононом, Досифєєм), і багато його праці збереглися завдяки дипломатичному листуванні з ними.
Коли народився Архімед, достовірно не відомо, а ось смерть його датується з абсолютною точністю. Він загинув в день взяття римлянами Сіракуз - рідного міста вченого. Це сталося в 212 р. До н.е. е. Вважається, що тоді йому було 75 років. Звідси виводиться рік народження Архімеда - 287 р. До н.е. е. Ми не знаємо чи був одружений, мав дітей і багато чого іншого. Але «від людини залишаються ... справи його» (М. Горький). Ось про діяння Архімеда і піде далі мова. Пам'ять поколінь донесла до нас досить, щоб судити про місце вченого в історії науки.
Архімед був родичем і другом царя Гієрона II (бл. 306 - 215 р. До н.е..), Який правив Сиракузамі більше 50 років. Це був розумний і далекоглядний політик, який умів ладнати з усіма своїми войовничими сусідами. Таємно підтримуючи Карфаген, Гиерон запевняв Рим у своїй вірності і слав «вічного міста» багаті подарунки. Це дозволило Сиракузам довгий час залишатися в стороні від безперервної боротьби Риму з Карфагеном за владу і вплив на Середземному морі.
Після смерті Гиерона трон успадкував його онук Гієронім.
Обидва правителя Сіракуз були тиранами, але в різному значенні цього слова. В молодості Гиерон був простим солдатом і на самий верх ієрархії піднявся тільки завдяки своєму розуму і особистої хоробрості. Це був освічений монарх (він навіть писав праці по сільському господарству).

Гиерон
Дуже детальну характеристику Гиерону дає давньоримський історик Полібій (210 - 130 рр. До н. Е.), Який народився всього через 5 років після смерті сиракузского царя: "Гиерон сам, власними силами придбав владу над Сіракузяне і союзниками, не маючи опори в багатстві , ні в славі, ні в будь-яких інших дарах долі. Згодом він нікого з городян не вбив, не виганяти, не образив і став царем сиракузян тільки завдяки своїм перевагам ... у продовженні 54-річного царювання Гиерон забезпечив мир для рідного міста, власну влада огородив від окушеній, уникнув заздрості, яка слід по стопах за всяким перевагою ... Всякий раз, коли він хотів скласти з себе владу, його утримували загальні прохання громадян. Дуже щедрий по відношенню до еллінам і ревнивий до доброго імені, він здобував самому собі гучну славу, а сіракузянам залишив в спадок загальне прихильність ".
Гиерон був тираном в сенсі «одноосібний правитель».
Онук його Гієронім відповідав іншим тлумаченням цього слова - «гнобитель, мучитель, деспот».

Гієронім
Як з'являються тирани і виникає тиранія? На це питання, яке хвилює нас, відповіли ще філософи давнини, попередники Архімеда: «Тиранія, - писав один з них, - це жахливе і мерзенне лихо, зобов'язана своїм походженням тільки тому, що люди перестали відчувати необхідність в загальному і рівному для всіх законі і право. Деякі люди, нездатні судити здраво, думають, що причини появи тиранів - інші і що люди позбавляються свободи без будь-якої провини з їх боку тільки тому, що стали жертвами насильства з боку висунувся тирана. Однак це помилка ... Як тільки потреба в загальному для всіх закон і право зникає з серця народу, на місце закону і права стає окрема людина ».
Сіракузяне недовго терпіли царювання Гієроніма - жорстокого і розпусного юнака. Незабаром він був убитий, а в місті проголошено республіку. Нові правителі Сиракуз уклали дружній союз з Карфагеном. Так рідне місто Архімеда виявився втягнутим у Другу Пунічної війну.
Більше 8 місяців (за іншими джерелами, близько 3 років) римське військо, очолюване консулом і полководцем Марком Клавдієм Марцеллом і проконсулом Аппієм Клавдієм, облягали Сіракузи з суші і моря, але не могло взяти місто, тому що на чолі оборони стояв Архімед.

АРХИМЕД
Автор «Римської історії» Тит Лівій (59 р. До н.е.. - 17 р. Н.е..) Пише: «Римляни, які взяли Леонтіни (місто на північ від Сіракуз) з першого ж натиску під дією тільки жаху, були цілком впевнені, що в якомусь місці вони прорвуться в обширний, розкиданий по великому простору місто, і приставили до стін всю готівку осадових машин. І розпочате з такою силою підприємство увінчалося б успіхом, якби в той час не було однієї людини. Цією людиною був Архімед ». Як військовий інженер, він заздалегідь підготувався до нападу ворога і побудував багато різних оборонних машин.
Уже згадуваний Полібій свідчить: «Архімед спорудив машини приспособительно до метання снарядів на будь-яку відстань. Так, якщо ворог підпливав видали, Архімед вражав його з далекобійних камнеметальніц важкими снарядами або стрілами і валив у скрутне безпорадне становище. Якщо ж снаряди починали літати поверх ворога, Архімед вживав в справу менші машини, кожен раз погодившись з відстанню, і наводив на римлян такий жах, що вони ніяк не наважувалися йти на приступ або наблизитися до міста на судах ».
Архімед винайшов і застосував ще інші механізми, про які Полібій пише: «... з машини пускалася прикріплена до ланцюга залізна лапа; керуючий жерлом машини захоплював цієї лапою ніс корабля в якомусь місці і потім всередині стіни опускав нижній кінець машини. Коли ніс судна був таким чином піднято і судно поставлено прямовисно на корму, підстава машини стверджувалося нерухомо, а лапа і ланцюг за допомогою мотузки відділялися від машини. Внаслідок цього деякі суду лягали на бік, інші зовсім перекидалися, треті (більшість) від падіння на них передніх частин зі значною висоти занурювалися в море, наповнювалися водою і приходили в розлад ».
Розповівши про те ж, Плутарх (бл. 45 - 127 м) додає: «Під кінець римляни були так налякані, що коли тільки бачили над стіною показуються колоду або мотузку, то кричали, що Архімед на них спрямовує якусь машину, відступали і зверталися у втечу ».
У античних письменників можна знайти повідомлення про те, що Архімед спалив ворожий флот за допомогою дзеркал. Цей факт довгий час піддавався сумніву, незважаючи на те що французький натураліст Ж. Л. Л. Бюффон (1707 - 1788) ще в 1747 р за допомогою великого дзеркала, що складається з багатьох невеликих плоских скляних дзеркал, кожне з яких направляло «зайчик» в одну точку, запалив дерево з відстані 50 м.
У 1973 р грецький інженер І. Сакас повторив досвід Бюффона, кілька видозмінивши його (наблизивши до однієї з легенд, яка стверджувала, що Архімед запалював римські кораблі, направляючи на них сонячне світло, відбите від полірованих мідних щитів грецьких воїнів). І. Сакс розставив по берегу кілька десятків солдатів, які тримали в руках плоскі дзеркала розміром 50х91 см. Спрямовані в одну точку сонячні промені підпалили човен, яка стояла в 50 м від берега. Так була остаточно доведена правдивість легенди про «запалювальних дзеркалах» Архімеда.
Багато місяців римляни стояли біля стін Сіракуз і так би не взяли місто, якби не свято богині Артеміди, який обложені відзначили дуже старанно. Вночі штурмовий загін римлян безшумно піднявся на стіни, перебив заснулу варту і увірвався в місто. Почалася різанина.
Деякі історики пишуть про зраду, завдяки якому римляни змогли захопити місто. Можливо, воно мало місце - адже осаждавшим якимось чином стало відомо, що захисники міста п'яні. А може бути, римляни просто знали про свято і здогадалися про його наслідки.
Розповідаючи про грабежі і насильства після Взяття Сіракуз, Тит Лівій пише: «Чимало прикладів брудної злоби і брудної жадібності можна було б пригадати, але найвідоміший між ними - Вбивство Архімеда. Серед дикого сум'яття, під крики і тупіт озвірілих солдатів, Архімед спокійно розмірковував, розглядаючи накреслені на піску фігури, і якийсь грабіжник заколов його мечем, навіть не підозрюючи, хто це ».

Плутарх повідомляє три версії загибелі вченого. «Цей геометр займався розглядом певної математичної фігури. Занурившись в споглядання, він не відчував ні бігання солдат, ні взяття міста. Аж ось перед ним воїн і повелів негайно слідувати за ним до Марцелл. Архімед не хотів, поки не вирішить завдання ... Розсерджений воїн оголив меч і вбив його. Інші кажуть, що на Архімеда напав римлянин з мечем в руках, щоб його вбити, і що Архімед, побачивши це, благав почекати, поки він не вирішить завдання, але вояк не уважив прохання вченого і позбавив його життя. Треті кажуть, що Архімед сам ніс Марцелл різні математичні прилади в ящику: сонячний годинник, небесний глобус і квадрант, яким вимірюють видиму величину Сонця, а впали йому назустріч воїни уявили, що в ящику золото, і вбили його ».

Ще про одну з легендою, пов'язаної зі смертю вченого, розповідає давньогрецький історик Діодор Сицилійський (бл. 80 - 29 м. До н.е..). Коли римський воїн схопив Архімеда, щоб тягнути його до Марцелл, геометр закричав: «Нехай хто-небудь з моїх соратників дасть мені будь-яка з моїх знарядь!». Римлянин злякався і вдарив, вченого мечем. Наказу про вбивство Архімеда не було. Відразу ж після взяття Сіракуз Марцелл дійсно наказав відшукати і привести до нього людини, який так довго і успішно протистояв йому, але було вже пізно. Консул наказав поховати вченого з усіма можливими почестями.

Смерть Архімеда. Гравюра з картини Едуарда Вімонта. Edouard Vimont (1846-1930)
Архімед як інженер прославився не тільки своїми військовими машинами. Він створив також водопідйомний гвинт (черв'як, равлика) і багатоступінчастий редуктор. Перший вживався як пристрій для підйому води протягом двох тисяч років. Ще в 20-х роках ХХ століття в Криму можна було побачити «архимедів черв'як», який застосовувався для відкачування густого соляного розчину. Архимедов гвинт послужив прототипом авіаційних пропелерів і суднових гвинтів.
Підйом предметів за допомогою Архимедова гвинта
Другий винахід використовувався для переміщення великих вантажів. Плутарх пише: «Архімед сказав якось своєму родичу і одному цареві Гиерону, що даної силою можна підняти будь-яку тяжкість. У сміливому довірі до сили свого докази він стверджував, що якби у нього була інша Земля, на яку можна було б перейти, то він зрушив би з місця нашу. Здивований Гиерон став просити його довести свої слова і привести в рух велике тіло малої силою. Архімед взяв царський вантажне судно, яке з великими труднощами і допомогою багатьох рук витягли було на берег, посадив на нього багато людей, поклав звичайний вантаж і, сидячи спокійно далеко, без найменшого зусилля, рухаючи тільки рукою кінець якоїсь складної машини, став тягти до себе судно так тихо і рівно, як ніби воно пливло по морю ». Історики науки припускають, що Архімед користувався в даному випадку багатоступеневим редуктором, який дає величезний виграш в силі.

Розповідають, що коли Гиерон побачив це «чудо», то він вигукнув: «З цього часу я вимагаю, щоб Архімеда вірили в усьому, що він тільки не скаже». Тепер - про наукову творчість вченого.
Архімед-математик першим обчислив площі еліпса і параболічного сегмента, площі поверхонь конуса і кулі, обсяги їх і сферичного сегмента, а також різних тіл обертання і їх частин. Він знайшов, що обсяги конуса і циліндра, що мають однакові підстави і висоту, відносяться як 1 до 3, а обсяги циліндра і вписаного в нього кулі - як 3 до 2. Цей останній отриманий ним результатrат Архімед вважав настільки важливим, що заповідав відобразити його на своєї могильній плиті, що і було виконано.

Куля, вписана в циліндр
Відповідний малюнок на камені бачив Полібій, який побував в Сіракузах через 50 років після смерті вченого.
Ще через 100 років відомий давньоримський державний діяч, оратор і письменник Марк Туллій Цицерон (106 - 43 рр. До н. Е.), Призначений на Сицилію квестором (помічником консула), тільки з цього помітного знаку знайшов покинуту могилу Архімеда на Сіракузькому кладовищі.
Цицерон пише: «Мені, квесторів, вдалося розшукати цю могилу, зарослу бур'янами травами і будяки; сіракузяни не тільки її не знали, але навіть заперечували її існування. Мені пам'ятали деякі вірші, про які я знав, що вони написані на його пам'ятнику; мені було також відомо, що вгорі його гробниці були вигравірувані куля і циліндр. Уважно вдивляючись ..., я помітив невелику колону, трохи виступаючу з кущів будяків; на ній було видно малюнок кулі і циліндра. Я сказав сіракузянам - мене супроводжували перші особи міста, - що це, мабуть, могила, яку я шукаю. Туди були послані люди з серпами, які очистили і розкрили це місце. Коли доступ став вільний, ми підійшли до підніжжя пам'ятника ... ». (Потім могила знову була забута, і в даний час місце поховання вченого невідомо.)
Передбачувана гробниця Архімеда в Сіракузах
Архімед досліджував спіраль спеціального виду, яка згодом була названа його ім'ям, показав, як можна побудувати дотичну до неї і знайти площу її витка. Він вирахував з великою точністю відношення довжини окружності до її діаметра (архимедова значення числа? Одно 22/7), дав теорію напівправильних опуклих багатогранників (архімедівських тел) і вивів формулу для визначення площі трикутника за його трьом сторонам (неправильно звану ім'ям Герона). Головне ж досягнення Архімеда в математиці полягає в тому, що, досліджуючи свою спіраль, він виступив як попередник творців методів диференціального обчислення, а вирішуючи завдання на знаходження площ і обсягів, застосовував методи, які пізніше (в кінці ХVI - початку ХVII ст.) Були названі методами неподільних і вичерпання і привели до створення інтегрального числення. Таким чином, в деяких питаннях математики Архімед випередив свій час на 18 століть!
Він справедливо писав: «... я думаю, що хто-небудь з теперішніх або майбутніх дослідників за допомогою запропонованого тут методу знайде і інші теореми, які нам не прийшли ще в голову».
Пояснимо «метод вичерпування» на прикладі того, як Архімед обчислював площу кола. Спочатку він вписав в нього шестикутник; потім на кожній стороні побудував трикутник - вийшов двенадцатіугольнік. Послідовно подвоюючи число сторін, Архімед отримав 24-кутник, 48-кутник і, нарешті, 96-кутник. Побудовані багатокутники все більш і більш покривали собою площу кола, як би поступово «вичерпуючи її. (Між іншим, цей метод знаходження площі круга до сих пір, через 2200 років після смерті Архімеда, викладається в сучасних шкільних підручниках геометрії).
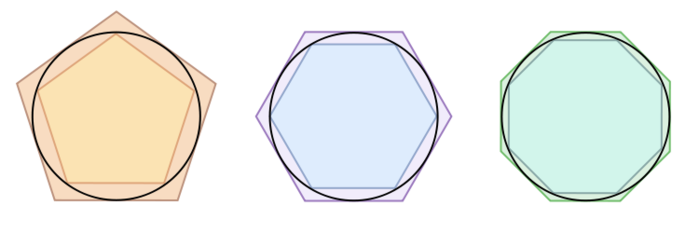
Обчислення площі кола методом вичерпування
Окремо серед математичних робіт Архімеда варто його «Обчислення піщинок в просторі, рівному кулі нерухомих зірок», або «Псамміт». Про мету, яку він переслідував, створюючи цю працю, вчений сам написав царю Гелону - синові і співправителя Герона II: «Є люди, які думають, що число піщинок нескінченно. Я не кажу про пісок в околиці Сіракуз і інших місцях Сицилії, але про все його кількості як в країнах населених, так і незаселених. Інші думають, що хоча число це і не нескінченно, але більшого уявити собі неможливо ... Я, навпаки, постараюся довести з геометричною точністю, яка переконає тебе, що ... є числа, що перевищують число піщинок, які можна вмістити не тільки в просторі, рівним обсягом 3емлі ... але і цілого світу ».
Греки позначали цифри літерами. Перші дев'ять букв алфавіту відповідали одиницям:? = 1,? = 2,? = 3 і т. Д., Наступні дев'ять букв зображували десятки:? = 10,? = 20,? = 30 і т. Д., Що залишилися літери - сотні. Так як в грецькому алфавіті менше 27 букв, то відсутні цифрові знаки позначалися комбінаціями букв. Тисяча відзначалася штрихом зліва від букви, десять тисяч називалися міріадой (позначалася літерою?). Мірнада була одиницею першого вищого розряду, за нею йшли одиниці, десятки, сотні і тисячі міріад.
Далі цього числа - в сучасній записи 104 • 104 = 108 (сто мільйонів) - греки не вважали. Архімед запропонував числа від 1 до 108 називати «першими числами». 3атем, приймаючи 108 за одиницю, він вводить «другі числа» - до 102 • 8, за ними слідують «треті числа» і т. Д.
Описати запропоновану ним систему числення, Архімед вірішує поставлених завдання. За його розрахунками в обсязі, який займає вся видима Всесвіт, міститься тисяча міріад «восьмих чисел» піщинок, що в сучасній записи відповідає числу 1063.
У фізиці давньогрецький вчений дав визначення центру ваги і показав, як його можна знайти для різних фігур і тіл. Йому належить математичний висновок закону рівноваги важеля. Це своє досягнення Архімед оцінив гордої фразою: «Дайте мені точку опори, і я зрушу 3емлю!».

Архімед перевертає планету Земля
У творі «Про рівновагу плоских фігур ...» Архімед вводить постулати, які очевидні і перевірені тисячолітньої практичною діяльністю.
«1. Рівні тяжкості на рівних довжинах врівноважуються, на нерівних ж довжина не врівноважуються, але переважують тяжкості на більшій довжині.
2. Якщо при рівновазі тягарів на якихось довжинах до однієї з тягарів буде що-небудь додано, то вони не будуть врівноважуватися, але переважить татяжесть, до якої було додано.
3. Точно так же якщо від однієї з тягарів буде відібрано що-небудь, то вони не будуть врівноважуватися, але переважить та тяжкість, від якої не було відібране ».
На підставі цих аксіом Архімед доводить закон рівноваги важеля: «Порівнянні величини врівноважуються на довжинах, які будуть обернено пропорційні тяжкості ... Якщо величини будуть несумірні, то вони точно так же уравновесятся на довжинах, які обернено пропорційні цим величинам». Під величинами Архімед розумів модулі сил, що діють на важіль.
Архімед ввів у фізику поняття питомої ваги і встановив один з основних законів гідростатики (згодом названий його ім'ям), який в сучасному формулюванні звучить так: «На всяке тіло, занурене в рідину, діє виштовхуюча сила, спрямована вгору і рівна вазі витісненої ним рідини» . (Чи справедливий і для газів.)
У роботі «Про плаваючих тілах» Архімед дає різні формулювання цього свого закону, як би приміряючись до нього з різних сторін. Одна з них говорить: «Тіла важчі, ніж рідина, опущені в цю рідину, будуть занурюватися, поки не дійдуть до самого низу, і в рідини стануть легше на величину ваги рідини в обсязі, рівному обсягу зануреного тіла».
Античні автори розповідають, що Архімед відкрив свій закон, коли лежав у ванні і розмірковував над вирішенням завдання, заданої йому Гиероном. Цар просив визначити, чи є в короні, зробленої придворним ювеліром, домішки інших металів або вона зроблена з чистого золота. Здогадавшись, як можна вирішити задачу, Архімед вискочив з ванни і з криком «Еврика!» ( «Знайшов!») Побіг вулицями міста.

Швидше за все це анекдот, один з багатьох, які люблять складати про великих людей. Але думка про спосіб визначення обсягу корони могла прийти вченому тоді, коли він занурювався в повну ванну і спостерігав за виливається з неї водою.
Архімед займався також оптикою (згадайте його «запальні дзеркала»), але праця, присвячена їй, не зберігся. Що цікавило вченого в цій галузі знання, нам відомо з робіт інших авторів: «Чому в плоских дзеркалах предмети зберігають свою натуральну величину, в опуклих - зменшуються, а в увігнутих - збільшуються; чому ліві частини предметів видно праворуч і навпаки; коли зображення в дзеркалі зникає і коли з'являється; чому увігнуті дзеркала, будучи поставлені проти Сонця, запалюють піднесений до них труть; чому в небі видно веселка; чому іноді здається, що на небі два однакових Сонця і багато іншого подібного ж роду, про що розповідається в об'ємистому томі Архімеда », - пише один з них.
Архімед прагнув все явища природи описати математично, тому його справедливо вважають родоначальником математичної фізики. Галілей прямо називає його своїм учителем.
Архімед-астроном постає перед нами, його нащадками, як теоретик, спостерігач-практик і творець різних астрономічних приладів. Якщо його уявлення про будову світу були помилкові, то точність його вимірювань за допомогою примітивних приладів вражає. Архімед першим намагався врахувати при знаходженні кутових розмірів небесних тіл і відстаней до них величину зіниці ока, він не приймав його за точку, як інші вчені. Архімед знайшов, що видимий діаметр Сонця укладений між 1/200 і 1/164 частками прямого кута (або між 27 і 35 хвилинами, в дійсності 32 '). Архімед дуже ясно і зрозуміло описує, як можна виміряти кутові розміри Сонця. «Зміцнивши довгу лінійку на вертикальній підставці, розташованої в місці, звідки видно схід Сонця, поставимо на лінійку вертикально невеликий точений циліндр. Коли Сонце близько до горизонту і на нього можна дивитися, лінійна повертається в бік Сонця і очей розташовується на краю лінійки. При цьому циліндр, перебуваючи між Сонцем і оком, закриває всі Сонце. Потім поступово переміщують циліндр від ока, поки Сонце не почне злегка реготати з усіх боків циліндра; на цьому місці циліндр закріплюється ».
Архімед точно визначив відстань до Венери, а до Марса і Меркурія - з помилкою в 5 і 8 відсотків відповідно. Це не тільки найбільш раннє з відомих нам визначень міжпланетних відстаней, а й залишалося довгий час найточнішим. Тит Лівій називає Архімеда «єдиним у своєму роді спостерігачем неба і зірок». (В той же час Архімед помилився, вираховуючи розміри Землі, відстань від Землі до Сонця і ставлення їх діаметрів.)
Особливо велике захоплення у сучасників і нащадків викликав створений Архімедом небесний глобус - прообраз теперішнього планетарію. У «Діалозі» Цицерона «Про державу» наведено розповідь одного зі співрозмовників - Луція Фурія Філа про цю дивовижну винахід вченого: «Я пам'ятаю, як Гай Сульпиций Галл ..., був в будинку у Марка Марцелла, який разом з ним колись був консулом, велів принести сферу, яку дід Марка Марцелла, завоювавши Сіракузи, вивіз із цього багатющого і розкішно прикрашеного міста, в той же час не доставивши звідти в свій будинок жодного іншого предмета з настільки значною військовою видобутку. Хоча я дуже часто чув розповіді про цю сферу, так як з нею було пов'язано славне ім'я Архімеда, сама вона не особливо подобалася мені; красивіша і більш відома в народі була інша сфера, створена цим же Архімедом, яку той же Марцелл віддав в храм Доблесті. Але коли Галл почав з великим знанням справи пояснювати нам пристрій цього приладу, я прийшов до висновку, що сицилиец володів хистом великим, ніж те, яким може володіти людина ... Коли Галл приводив цю сферу в рух, відбувалося так, що на цій кулі з бронзи Місяць змінювала Сонце протягом стількох же обертів, у скільки днів вона змінювала його на самому небі ».
Римський поет V ст. Клавдіан, також бачив «сферу», присвятив їй такі рядки:
«Неба статут, закони богів, гармонію світу-
Все Сіракузького старий мудро на землю приніс.
Повітря, прихований всередині, різні рухає світила
Точно по дивним шляхах, зробивши творіння живим ».
Звідси випливає, що «сфера» приводилася в рух якимось пневматичним механізмом. Створення небесного глобуса - ще одне свідчення того, що Архімед був видатним винахідником.

«Архімед». Доменіко Фетті, 1620
На закінчення наведемо портрет вченого, намальований Плутархом: «Архімед мав піднесену душу і глибокий розум ... У всій геометрії не можна знайти більш важких і глибокодумних завдань, які були б вирішені так просто і ясно, як ті, які були предметом досліджень Архімеда .. . Чи не здається неймовірним, що він, як розповідають, будучи зачарований геометрією як якийсь домашньої сиреною, забував про їжу, питво і нехтував турботами про своє тіло; нерідко насильно тягли його в баню і до натирання маслом, але він і в лазні на вогнищі зображував геометричні фігури, а по своєму тілу, намазати маслом, креслив пальцем лінії ... Хоча у нього було багато прекрасних відкриттів, він, кажуть, просив своїх родичів і друзів накреслити на його могилі тільки циліндр і вписаний в нього кулю і вказати співвідношення між обсягами цих тіл. Такий був Архімед, який завдяки своїм глибоким знанням в механіці зміг, наскільки це від нього залежало, зберегти від ураження і себе, і своє місто »...

Зображення Архімеда на медалі Філдса
Філдсовськая премія (англ. Fields Medal) - міжнародна премія і медаль, які вручаються один раз в 4 роки на кожному міжнародному математичному конгресі двом, трьом або чотирьом молодим математикам не старші 40 років (або досягли 40-річчя в рік вручення премії).
Текст: interlibrary.narod.ru

Спіраль Архімеда і її прояви в навколишньому світі
Тетяна Варава
Спіраль, незважаючи на простоту зображення, - це складний і ємний за значенням символ. Ще древні люди використовували її як декоративний символ, візерунок, легко наноситься на дерево, каміння, глину. Форма спіралі поєднує в собі симетрію і золотий перетин, при зоровому сприйнятті вона викликає відчуття гармонії і краси. Спіраль, пов'язана з символікою центру, здавна є початком почав, звідки стартує еволюція, розвиток, рух життя. Свого часу на її форму звернув увагу Архімед. Давньогрецький вчений з Сіракуз вивчив форму спірально закрученою раковини і вивів рівняння спіралі. Накреслений ним з цього рівняння виток названий його ім'ям - спіраль Архімеда.
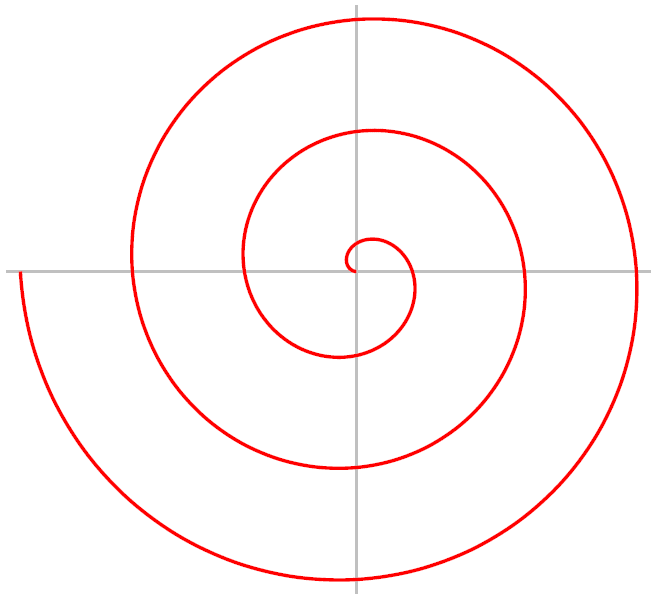
виток Архімеда
Крива, яку описує точка, що рухається з постійною швидкістю вздовж променя, що обертається з незмінною кутовою швидкістю навколо свого початку, називається так: "спіраль Архімеда". Побудова її проводять наступним чином: ставлять її крок - а, проводять з центру Про коло радіусом, рівним кроку спіралі, крок і окружність ділять на кілька рівних частин, нумеруя точки ділення.

Архімед в своєму трактаті «Про спіралі» досліджував властивості даної форми, використовуючи полярні координати, він записав характеристичне властивість її точок, дав побудову дотичної до спіралі і визначив її площа. Відображає спіраль Архімеда формула r = a * theta. Вчений знав, що збільшення кроку спіралі завжди рівномірно.
символічність
Вражає надзвичайна розмаїтість значень символу спіралі. Він сприймається як хід і плин часу (циклічні ритми, зміна сонячних і місячних фаз, хід історії, людського життя). Спіраль вважається знаком розвитку, життєвої сили, даної нам природою. Це прагнення до нових рівнів, до свого центру, мудрості. Спіраль часто асоціюється зі змією, яка уособлювала, в свою чергу, мудрість предків. Адже відомо, що змії дуже люблять згортатися кільцями і зовні схожі на спіралі.

У природі спіраль проявляється в трьох основних формах: застиглої (раковини равлика), що розширюється (зображення спіральних галактик) або стискується (подобу виру). Спіральні форми представлені від еволюційних глибин (молекули ДНК) до законів діалектики.
Спіраль близька до кола - самої ідеальній формі з усіх, що створила природа. Дійсно, стихійні і природні елементи, які мають форму спіралі, дуже поширені в природі. Це спіральні туманності, галактики, вири, смерчі, торнадо, пристрої рослин. Навіть павуки спиралеобразно плетуть павутину, закручуючи нитки по спіралі навколо центру. Природа любить повторення, в її творах використані одні й ті ж принципи.
Спіраль Архімеда і послідовність Фібоначчі

Спіраль Архімеда має тісний зв'язок з послідовністю Фібоначчі. Даний закон математики описує принцип спіралі Архімеда і золотого перетину. Їх тісний зв'язок можна спостерігати у багатьох явищ і елементів природи - в пристрої раковини молюсків, суцвіть соняшнику і сукулентних рослин, фрактальної капусти і соснових шишок, людини і цілих галактик.
спіральна симетрія
Фактор часу, що поєднується з обертанням і спрямованим рухом, формує форму спіралі. Спіралі, присутні в структурі творів мистецтва, мають відношення до часу, не до простору. Вони присутні в основному в узорах, рідше - в архітектурі. Це шпилі соборів і гвинтові сходи.

Застосування в техніці
Спіраль Архімеда в даний час широко використовується в техніці. Одне з винаходів ученого - гвинт (прообраз об'ємної спіралі) - використовувалося як механізм для передачі води в зрошувальні канали з низьколежачих водойм. Гвинт Архімеда став прообразом шнека ( «равлики») - пристрої, широко використовуваного в різних машинах для перемішування рідких, сипучих і тістоподібних матеріалів. Найпоширеніша його різновид - гвинтовий ротор у звичайній м'ясорубці. Прикладом застосування в техніці Архімедова спіралі також є самоцентруючийся патрон. Даний механізм використовується в швейних машинках для рівномірного намотування ниток.
Нині спіраль Архімеда заслуговує на особливу увагу при навчанні комп'ютерної графіки.

Володимир Долгов. «Птах-Фенікс» або «Спіраль Архімеда в екстазі Червоного півня"

Перші дев'ять букв алфавіту відповідали одиницям:?
Наступні дев'ять букв зображували десятки:?
Позначалася літерою?




