
| Головна сторінка | Інструкція користувача | Практикум абітурієнта | Навчальні програми |
| математичний гурток | Цікава математика | Формули, словники | Новини |
| сторінки історії | Іспити, тести | Бібліографія | посилання | Мапа |
Лінійні рівняння і нерівності з параметром
рівняння виду
де a, b Про R, x - змінна, називається рівнянням першого ступеня (лінійним рівнянням).Нижче наведені приклади лінійних рівнянь:
a) 2 x + 6 = 0, де a = 2, b = 6; b) x - 2 = 0 де a = 1, b = -2; c) 0 · x + 0 = 0, де a = b = 0; d) 0 · x + 1/3 = 0, де a = 0, b = 1/3; e) -1/2 x = 0, де a = -1/2; b = 0.рівняння ( 1 ) Рівносильне рівнянню
ax = - b звідки слід наступне твердження.Затвердження 1.
- Якщо a ≠ 0, то рівняння ( 1 ) Має єдине рішення x = -b / a;
- Якщо a = 0, b ≠ 0, то безліч рішень рівняння ( 1 ) Порожньо;
- Якщо a = 0, b = 0, то будь-яка дійсна число є рішенням рівняння ( 1 ).
Таким чином, наведені вище лінійні рівняння вирішуються наступним чином:
a) x = -6/2, тобто x = -3;
b) x = 2;
c) будь-яке дійсне число є рішенням даного рівняння;
d) рівняння не має рішень;
e) x = 0.
Зауваження 1. Рівняння
ax + b = cx + d, де a, b, c, d Про R, зводиться до лінійного рівняння ( 1 ): Ax + b = cx + d И (a - c) x + (b - d) = 0, або ax + b = cx + d И (a - c) x = d - b.Зауваження 2. Рівняння
(Ax + b) (cx + d) = 0 де a, b, c, d Про R, зводиться до сукупності лінійних рівняньПриклад 1. Вирішити рівняння
Рішення. a) 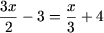
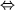
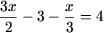
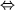
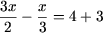
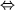
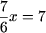
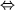
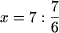
 x = 6.
x = 6.
b) 2 x + 1 = 2 x + 3 И 2 x - 2 x = 3 - 1 И 0 · x = 2 звідки випливає, що рівняння не має рішень.
c) - x + 2 = 2 - x И - x + x = 2 - 2 И 0 · x = 0, отже, будь-яка дійсна число є рішенням рівняння.
d) (2 x + 4) (3 x - 1) = 0 И ИНадалі будуть розглядатися лінійні рівняння з параметрами. Під параметром розуміється (дивіться тему Рівняння з параметром) фіксоване (але невідоме) число. Як правило, параметр позначається першими літерами латинського алфавіту.
Приклад 2. Вирішити рівняння
Рішення. a) Застосовуючи твердження 1 , Отримаємо:
при a ≠ 0 рівняння має єдине рішення, x = 1 / a;
при a = 0 рівняння набуде вигляду 0 · x = 1 і, отже, воно не має рішень.
Відповідь: якщо a Про R \ {0}, то x = 1 / a; якщо a = 0, то рівняння не має рішень.
b) Після елементарних перетворень отримаємо:
a 2 x - 1 = x + a И a 2 x - x = a + 1 И x (a 2 - 1) = a + 1.звідки, застосовуючи твердження 1 , Отримаємо:
- якщо a 2-1 ≠ 0, тобто a ≠ ± 1, то
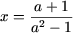 або
або 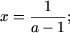
- якщо a = 1, то рівняння набуде вигляду 0 · x = 2 і, отже, не має рішень;
- якщо a = -1, то рівняння набуде вигляду 0 · x = 0, і, отже, будь-яка дійсна число є вирішенням цього рівняння.
c) Перепишемо рівняння таким чином
(A - c) x = d - b, звідки слід:- якщо a - c ≠ 0, тобто a ≠ c, то рівняння має єдине рішення
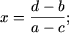
- якщо a = c і d - b ≠ 0, то рівняння набуде вигляду 0 · x = d - b (≠ 0) і, отже, воно не має рішень;
- якщо a = c і d = b, то рівняння набуде вигляду 0 · x = 0, і, отже, безліч його рішень є R
d) Область допустимих значень (ОДЗ) рівняння є x ≠ 4. У ОДЗ рівняння вирішується таким чином:
Таким чином, якщо 2 a ≠ 4, тобто a ≠ 2, то рівняння має єдине рішення x = 2 a, а якщо a = 2, то рівняння не має рішень.
e) ОДЗ рівняння є безліч R \ {- 1; 2}. Оскільки (x - a) (2 x + a) = 0 тягне x 1 = a і x 2 = -a / 2, так як x ≠ -1 і x ≠ 2, отримаємо:
- якщо a ≠ -1, a ≠ 2, -a / 2 ≠ -1, -a / 2 ≠ 2, тобто a Про R \ {- 1; 2; -4}, то рівняння має два рішення x 1 = a і x 2 = -a / 2 (якщо a = 0, рішення збігаються);
- якщо a = -1, то рівняння має єдине рішення x = 1/2;
- якщо a = 2, то рівняння не має рішень;
- якщо a = -4, то рівняння має єдине рішення x = -4.
f) Якщо a = 0 або b = 0, то рівняння не має сенсу. Нехай a · b ≠ 0. Тоді рівняння рівносильне наступному
x (b + a) = abc звідки слід:- якщо b + a ≠ 0, тобто a ≠ - b, то рівняння має єдине рішення
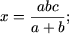
- якщо a = - b і c ≠ 0, то рівняння не має рішень.
- якщо a = - b і c = 0, то будь-яка дійсна число є рішення даного рівняння.
g) ОДЗ рівняння визначається з системи
звідки x ≠ a / 5 і, якщо a ≠ 0, x ≠ 1 / a. Якщо a = 0, то рівняння набуде вигляду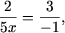 або -2 = 15 x,
або -2 = 15 x, звідки 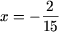 , І, оскільки
, І, оскільки 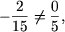 випливає, що якщо a = 0 то рівняння має рішення
випливає, що якщо a = 0 то рівняння має рішення 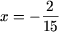 .
.
Нехай a ≠ 0. Тоді в ОДЗ рівняння набуде вигляду
2 (ax - 1) = 3 (5 x - a), звідки (2 a - 15) x = 2 - 3 a і, отже,- якщо 2 a - 15 ≠ 0, тобто
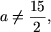 то отримаємо
то отримаємо 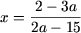 ;
; - якщо 2 a -15 = 0, тобто
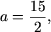 то рівняння не має рішень.
то рівняння не має рішень.
Таким чином для 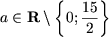 потрібно перевірити умову x ≠ a / 5 і x ≠ 1 / a:
потрібно перевірити умову x ≠ a / 5 і x ≠ 1 / a:
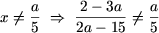 або (2 a - 15) a ≠ 5 (2 - 3 a) звідки 2 a 2 ≠ 10, або
або (2 a - 15) a ≠ 5 (2 - 3 a) звідки 2 a 2 ≠ 10, або 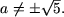 Таким чином, для
Таким чином, для 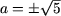 рівняння не має рішень.
рівняння не має рішень. У разі другого обмеження отримаємо
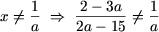 або a (2 - 3 a) ≠ (2 a - 15), звідки 3 a 2 = 15, тобто a 2 ≠ 5 (вже досліджений випадок).
або a (2 - 3 a) ≠ (2 a - 15), звідки 3 a 2 = 15, тобто a 2 ≠ 5 (вже досліджений випадок). Таким чином, якщо 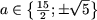 рівняння не має рішень, а якщо
рівняння не має рішень, а якщо 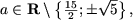 то рівняння має єдине рішення
то рівняння має єдине рішення
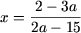 (зауважимо, що рішення отримане в разі a = 0 міститься в наведеному вище результаті).
(зауважимо, що рішення отримане в разі a = 0 міститься в наведеному вище результаті). Приклад 3. Вирішити рівняння
a) | x - a | = 2; c) | x - a | + | x - 2 a | = A; b) | x | + | x - a | = 0; d) | x - 1 | + | x - 2 | = A.Рішення. a) Використовуючи властивість модуля, одержимо:
| x - a | = 2 И И Таким чином, для будь-якого дійсного a рівняння має два різних рішення, x 1 = a + 2 і x 2 = a - 2.b) Ліва частина рівняння приймає невід'ємні значення (як сума двох невід'ємних складових), а права частина дорівнює нулю. отже,
Таким чином, якщо a = 0, то система (а, отже, і рівняння) має єдине рішення x = 0, а якщо a ≠ 0, то система (і вихідне рівняння) рішень не має.
c) Так як | f (x) | = | - f (x) | рівняння можна переписати таким чином
| x - a | + | 2 a - x | = A.Очевидно, що якщо a a = 0, то отримаємо | x | = 0, звідки x = 0.
Нехай a> 0. Тоді a = | a | = | (2 a - x) + (x - a) |, і рівняння набуде вигляду
| x - a | + | 2 a - x | = | (2 a - x) + (x - a) |. Це рівняння рівносильне (див. Властивості модуля) нерівності (2 a - x) (x - a) ≥ 0 звідки, враховуючи, що 0 aa, отримаємо рішення x О [a; 2 a].Таким чином:
якщо a якщо a = 0, то рівняння має єдине рішення x = 0;
якщо a> 0, то рівняння має нескінченну кількість рішень - будь-яке число
a ≤ x ≤ 2 a.d) Очевидно, що рівняння має рішення тільки при a> 0. Розглянемо три випадки:
- Нехай x x - 1 | = - (x - 1), | x - 2 | = - (x - 2) і рівняння набуде вигляду - x + 1 - x + 2 = a або -2 x = a - 3 звідки
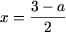 . оскільки x
. оскільки x 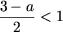 звідки a> 1. Таким чином, якщо a> 1, то
звідки a> 1. Таким чином, якщо a> 1, то 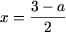 ;
; - Нехай x О [1; 2]. тоді | x - 1 | = X - 1, | x - 2 | = - (x -2) і рівняння набуде вигляду x - 1 - x + 2 = a, 0 · x = a - 1. Використовуючи твердження 1 , Отримаємо:
якщо a = 1, то будь-яка дійсна число з відрізка [1; 2] є рішення вихідного рівняння;
якщо a ≠ 1, то рішень немає.
- Нехай x> 2. Тоді | x - 1 | = X - 1, | x - 2 | = X - 2 і рівняння набуде вигляду x - 1 + x - 2 = a звідки
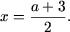 Оскільки x> 2, то
Оскільки x> 2, то 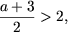 тобто a> 1.
тобто a> 1. Таким чином:
якщо a> 1, то рівняння має два різних рішення
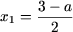 і
і 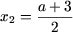
якщо a = 1, то будь-яке число відрізка [1; 2] є рішення рівняння;
якщо a
лінійні нерівностінерівності виду
ax + b> 0, ax + b ≥ 0, ax + b ax + b ≤ 0, (2) де a, b Про R, x - змінна, називаються нерівностями першого ступеня (лінійними нерівностями).Оскільки всі нерівності ( 2 ) Вирішуються аналогічно, наведемо рішення лише першого з них: ax + b> 0. Розглянемо наступні випадки:
- a> 0, тоді ax + b> 0 И ax> - b И x> -b / a і, отже, безліч рішень нерівності ax + b> 0 (a> 0) є (-b / a; + Ґ);
- a ax + b> 0 И ax> - b И x b / a і, отже, безліч рішень нерівності ax + b> 0 (a Ґ; -b / a);
- a = 0, тоді нерівність прийме вигляд 0 · x + b> 0 і для b> 0 будь-яка дійсна число є рішення нерівності, а при b ≤ 0 нерівність не має рішень.
Розглянемо кілька прикладів.
Приклад 1. Вирішити нерівності
a) 3 x + 6> 0; c) 2 (x + 1) + x x + 1; b) -2 x + 3 ≥ 0; d) 3 x + 2 ≥ 3 (x - 1) + 1.Рішення. a) 3 x + 6> 0 И 3 x> -6 И x> -2, і, отже, безліч рішень вихідного нерівності є (-2; + Ґ).
b) -2 x + 3 ≥ 0 И -2 x ≥ -3 И x ≤ 3/2, тобто безліччю рішень вихідного нерівності є (- Ґ; 3/2].
c) Після елементарних перетворень отримаємо лінійне нерівність
2 (x + 1) + x x + 1 И 2 x + 2 + x x + 1 И 0 · x + 1 Так як 1 d) Вирішуючи аналогічно прикладу c), отримаємо 3 x + 2 ≥ 3 (x - 1) + 1 И 3 x + 2 ≥ 3 x - 3 + 1 И 0 · x + 4 ≥ 0, звідки випливає, що будь-яка дійсна число є рішенням вихідної нерівності.Приклад 2. Вирішити нерівності
Рішення. a) У залежності від знака a розглянемо три випадки:
- якщо a> 0, то x ≤ 1 / a;
- якщо a x ≥ 1 / a;
- якщо a = 0, то нерівність набуде вигляду 0 · x ≤ 1 і, отже, будь-яка дійсна число є рішенням вихідної нерівності.
Таким чином, якщо a> 0, то x О (- Ґ; 1 / a], якщо a x О [1 / a; + Ґ), і якщо a = 0, то x Про R.
b) Зауважимо, що | x - 2 | ≥ 0 для будь-якого дійсного x і - (a -1) 2 ≤ 0 для будь-якого значення параметра a. Отже, якщо a = 1, то будь-який x дійсне число, відмінне від 2, є рішенням нерівності, а якщо a ≠ 1, то будь-яка дійсна число є рішенням нерівності. Відповідь: якщо a = 1, то x Про R \ {2}, а якщо a Про R \ {1}, то x Про R.
c) Після елементарних перетворень отримаємо
3 (4 ax) ax + 3 И 12 a - 3 x ax + 3 И 12 a - 3 ax + 3 x И x (2 a + 3)> 3 (4 a - 1).Далі розглянемо три випадки:
- якщо 2 a + 3> 0, тобто a> -3/2, то
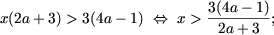
- якщо 2 a + 3 a 3/2, то
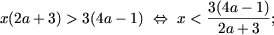
- якщо 2 a + 3 = 0, тобто a = -3/2, то нерівність набуде вигляду 0 · x> -21 і, так як 0> -21 - справжнє числове нерівність, слід, що будь-яка дійсна число є рішенням вихідної нерівності .
отже,
якщо
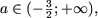 то
то 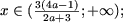
якщо
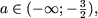 то
то 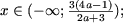
якщо a = -3/2, то x Про R.
d) abx + b> ax + 3 И abx - ax> 3 - b И a (b - 1) · x> 3 - b.
Далі розглянемо такі випадки:
- якщо a (b - 1)> 0, тобто a> 0 і b> 1, або a b
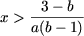
- якщо a (b - 1) a> 0 і b ab> 1, то
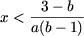
- якщо a = 0, b ≠ 1 то нерівність набуде вигляду 0 · x> 3 - b і для b> 3 будь-яке число є рішенням, а якщо b О (- Ґ; 1) І (1; 3], то безліч рішень нерівності порожньо.
- якщо a ≠ 0, b = 1, то нерівність набуде вигляду 0 · x> 2 і, очевидно, що воно рішень не має.
отже,
якщо a> 0 і b> 1, або a b
якщо a> 0 і b ab> 1, то 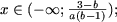
якщо a = 0 і b О (3; + Ґ), то x Про R;
якщо a = 0 і b О (- Ґ; 1) І (1; 3) чи a ≠ 0 і b = 1, то нерівність не має рішень.
e) Зауважимо, що a ≠ ± 1, (в іншому випадку нерівність не має сенсу). Нерівність переписується в такий спосіб
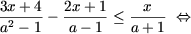
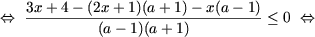
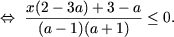
Далі розглянемо такі випадки:
1. нехай a О (- Ґ; -1) І (1; + Ґ), тоді (a - 1) (a + 1)> 0 і, отже, вихідне нерівність рівносильне наступному
x (2 - 3 a) + 3 - a ≤ 0, або x (2 - 3 a) ≤ a - 3, звідки для a> 1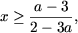 для a
для a 2. нехай a О (-1; 1), тоді (a - 1) (a + 1) x (2 - 3 a) + 3 - a ≥ 0 або x (2 - 3 a) ≥ a - 3.
Остання нерівність виконується в такий спосіб:
якщо a = 2/3, то x Про R
якщо a О (-1; 2/3), то 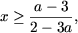
якщо a О (2 / 3,1), то 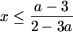 .
.
Таким чином, вихідне нерівність
при a О (- Ґ; -1) І (2/3; 1) має рішення 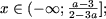
при a О (-1; 2/3) І (1; + Ґ) має рішення 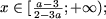
при a = 2/3, будь-яка дійсна число є рішенням вихідної нерівності.
f) Початкове нерівність рівносильне наступному
(A - c) x> d - b звідки випливає, що- якщо a> c, то a - c> 0 і, отже,
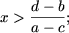
- якщо a c, то
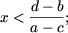
- якщо a = c і d ≥ b, то безліч рішень нерівності порожньо;
- якщо a = c і d b, то x Про R.
g) Зауважимо, що a ≠ 0 і b ≠ 0. Привівши до спільного знаменника, одержимо
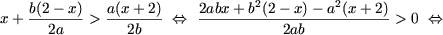
Таким чином, якщо a і b одіннакогого знака (ab> 0) і a ≠ b, то безліч рішень нерівності є 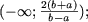 якщо a і b - протилежних знаків (ab а якщо a = b то нерівність не має рішень.
якщо a і b - протилежних знаків (ab а якщо a = b то нерівність не має рішень.
Приклад 3. Вирішити нерівності
a) | x + a | + | x - 2 a | a; c) | x + a | > 2; b) | x + a | a | x; d) | x - a | ≤ a.Рішення. a) Зауважимо, що при a ≤ 0 нерівність рішень не має. Нехай a> 0. Розглянемо три випадки:
- нехай x О (- Ґ; - a], тоді | x + a | = - x - a і | x - 2 a | = 2 a - x і нерівність набуде вигляду - x - a + 2 a - x a, або x> -3/2 a, оскільки a> 0, перетином множин (- Ґ; - a] і
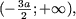 (А, отже, і безліччю рішень нерівності) явяется безліч
(А, отже, і безліччю рішень нерівності) явяется безліч 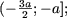
- нехай x О (- a; 2 a], тоді | x + a | = x + a, і | x - 2 a | = 2 a - x, і нерівність набуде вигляду x + a + 2 a - x a або 3 a a і, оскільки a> 0, будь-яке число з інтервалу (- a; 2 a] є рішення нерівності;
- нехай x О (2 a; + Ґ), тоді | x + a | = X + a і | x - 2 a | = X - 2 a, і нерівність набуде вигляду x + a + x - 2 a a або x 5/2 a. З огляду на умова x> 2 a, отримаємо x О (2 a; 5/2 a).
Таким чином, якщо a ≤ 0, то нерівність не має рішень, а якщо a> 0, то безліч рішень нерівності є (-3/2 a; - a] І (- a; 2 a] І (2 a; 5 / 2 a) або (-3/2 a; 5/2 a).
b) Зауважимо, що нерівність може мати лише позитивні рішення. Для x> 0 нерівність переписується | x + a | a | · | x | і вирішується, використовуючи властивості модуля:
| x + a | a | · | x | И | x + a | ax | И (x + a + ax) (x + a - ax) И И [(a + 1) x + a] [(1 - a) x + a] И ИЯкщо a> 1, тоді a - 1> 0 і a + 1> 0, і перша система сукупності набуде вигляду
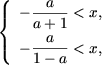 звідки (з огляду на, що x> 0) отримаємо
звідки (з огляду на, що x> 0) отримаємо 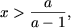 а друга система сукупності набуде вигляду
а друга система сукупності набуде вигляду 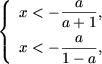 і, так як a> 1 тягне
і, так як a> 1 тягне 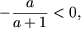 а x> 0, система не має рішень.
а x> 0, система не має рішень. Якщо a = 1, то перша система сукупності не має рішень, а з другої отримаємо x 1/2, і, так як x> 0, то і в цьому випадку вихідне нерівність не має рішень.
Якщо -1 aa + 1> 0 і 1 - a> 0, і перша система сукупності набуде вигляду
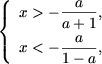 або
або 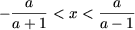 звідки, помітивши, що
звідки, помітивши, що 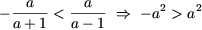 отримаємо, що перша система сукупності несовместна. З другої системи отримаємо
отримаємо, що перша система сукупності несовместна. З другої системи отримаємо 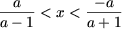 і, з огляду на, що x> 0, отримаємо
і, з огляду на, що x> 0, отримаємо 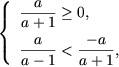 звідки a a О [0; 1), то нерівність не має рішень, а якщо a О (-1; 0), то безліч рішень нерівності є
звідки a a О [0; 1), то нерівність не має рішень, а якщо a О (-1; 0), то безліч рішень нерівності є 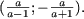
Якщо a = -1, то перша система сукупності несовместна, а з другої отримаємо x> 1/2.
Якщо a a + 1 a> 0, і з першої системи слід
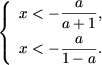 Так як a а x> 0, то в цьому випадку вихідне нерівність не має рішень. Друга система сукупності набуде вигляду
Так як a а x> 0, то в цьому випадку вихідне нерівність не має рішень. Друга система сукупності набуде вигляду 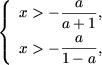 і, оскільки x> 0, отримаємо
і, оскільки x> 0, отримаємо 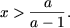
Таким чином,
якщо a О (- Ґ; -1) І (1; + Ґ), то 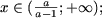
якщо a О [0; 1], то нерівність не має рішень;
якщо a = -1, то x О (1/2; + Ґ).
c) Використовуючи властивість модуля, одержимо
| x + a | > 2 И Иd) Якщо a a = 0, то нерівність має єдине рішення: x = 0. Якщо a> 0, то
| x - a | ≤ a И - a ≤ x - a ≤ a И 0 ≤ x ≤ 2 a.| Головна сторінка | Інструкція користувача | Практикум абітурієнта | Навчальні програми |
| математичний гурток | Цікава математика | Формули, словники | Новини |
| сторінки історії | Іспити, тести | Бібліографія | посилання | Мапа |





