Турбул е нтность, явище, яке спостерігається в багатьох течіях рідин і газів і полягає в тому, що в цих течіях утворюються численні вихори різних розмірів, унаслідок чого їх гідродинамічні і термодинамічні характеристики (швидкість, температура, тиск, щільність) випробовують хаотичні флуктуації і тому змінюються від точки до точки і в часі нерегулярно. цим турбулентні течії відрізняються від так званих ламінарних течій . Більшість течій рідин і газів в природі (рух повітря в земній атмосфері, води в річках і морях, газу в атмосферах Сонця і зірок і в міжзоряних туманностях і т.п.) і в технічних пристроях (в трубах, каналах, струменях, в прикордонних шарах близько рухомих в рідині або газі твердих тіл, в слідах за такими тілами і т.п.) виявляються турбулентними.
Завдяки великій інтенсивності турбулентного перемішування турбулентні течії мають підвищену здатність до передачі кількості руху (І тому до підвищеного силового впливу на обтічні тверді тіла), передачі тепла, прискореному поширенню хімічних реакцій (зокрема, горіння), здатністю нести і передавати зважені частинки, розсіювати звукові і електромагнітні хвилі і створювати флуктуації їх амплітуд і фаз, а в разі електропровідної рідини - генерувати флуктуірует магнітне поле і т.д.
Т. виникає внаслідок гідродинамічної нестійкості ламінарного течії, яке втрачає стійкість і перетворюється в турбулентний, коли так зване Рейнольдса число Re = l u / n перевершить деяке критичне значення Rekp (l і u - характерні довжина і швидкість в даному перебігу, n - кінематичний коефіцієнт в'язкості). За експериментальними даними, в прямих круглих трубах при найбільшій можливій мірі обуреності течії біля входу в трубу Rekp »2300 (тут l - діаметр труби, u - середня по перерізу швидкість). Зменшуючи ступінь початкової обуреності течії, можна домогтися затягування ламінарного режиму до значно більших Rekp, наприклад в трубах до Re kp »50 000. Аналогічні результати отримані для виникнення Т. в прикордонному шарі .
Виникнення Т. при обтіканні твердих тіл може виявлятися не тільки у вигляді турбулізації пограничного шару, але і у вигляді освіти турбулентного сліду за тілом в результаті відриву прикордонного шару від його поверхні. Турбулізація прикордонного шару до точки відриву приводить до різкого зменшення повного коефіцієнта опору тіла. Т. може виникнути і далеко від твердих стінок, як при втраті стійкості поверхні розриву швидкості (наприклад, утворюється при відриві прикордонного шару або є кордоном затопленого струменя або поверхнею розриву щільності), так і при втраті стійкості розподілу щільності шарів рідини в полі тяжіння, то тобто при виникненні конвекції . Дж. У. Релей встановив, що критерій виникнення конвекції в шарі рідини завтовшки h між двома площинами з різницею температур d T має вигляд Ra = g bh 3 d T / nc, де g - прискорення сили тяжіння, b - коефіцієнт теплового розширення рідини, c - коефіцієнт її температуропровідності . Критичне число Релея Rakp має значення близько 1100-1700.
Внаслідок надзвичайної нерегулярності гідродинамічних полів турбулентних течій застосовується статистичний опис Т .: гідродинамічні поля трактуються як випадкові функції від точок простору і часу, і вивчаються розподілу ймовірностей для значень цих функцій на кінцевих наборах таких точок. Найбільший практичний інтерес представляють найпростіші характеристики цих розподілів: середні значення і другі моменти гідродинамічних полів, в тому числі дисперсії компонент швидкості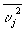 
(де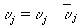 
пульсації швидкості, а риска вгорі - символ осреднения); компоненти турбулентного потоку кількості руху 
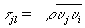(Так зване напруги Рейнольдса) і турбулентного потоку тепла 
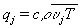(r - щільність, з - питома теплоємність, Т - температура). Статистичні моменти гідродинамічних полів турбулентного потоку повинні задовольняти деяким рівнянням (що випливають з рівнянь гідродинаміки), найпростіші з яких - так звані рівняння Рейнольдса, виходять безпосереднім осреднением рівнянь гідродинаміки. Однак точного рішення їх досі не знайдено, тому використовуються різні наближені методи.
Основний внесок в передачу через турбулентне середовище кількості руху і тепла вносять великомасштабні компоненти Т. (масштаби яких порівнянні з масштабами течії в цілому); тому їх опис - основа розрахунків опору і теплообміну при обтіканні твердих тіл рідиною або газом. Для цієї мети побудований ряд так званих напівемпіричних теорій Т., в яких використовується аналогія між турбулентним і молекулярним перенесенням, вводяться поняття шляху перемішування, інтенсивності Т., коефіцієнта турбулентної в'язкості і теплопровідності і приймаються гіпотези про наявність лінійних співвідношень між напруженнями Рейнольдса і середніми швидкостями деформації , турбулентним потоком тепла і середнім градієнтом температури. Така, наприклад, застосовується для плоскопараллельного осредненного руху формула Буссінеска t = Ad u / dy з коефіцієнтом турбулентного перемішування (турбулентної в'язкості) А, який, на відміну від коефіцієнта молекулярної в'язкості, вже не є фізичною постійною рідини, а залежить від характеру усередненого руху. На підставі напівемпіричної теорії Прандтля можна прийняти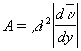 
, Де шлях перемішування l - турбулентний аналог довжини вільного пробігу молекул.
Велику роль в напівемпіричних теоріях грають гіпотези подібності (див. подібності теорія ). Зокрема, вони служать основою напівемпіричної теорії Кармана, по якій шлях перемішування в плоскопаралельному потоці має вигляд l = - cu '/ u' ', де u = u (у) - швидкість течії, а c - постійна. А. Н. Колмогоров запропонував використовувати в напівемпіричних теоріях гіпотезу подібності, по якій характеристики Т. виражаються через її інтенсивність b і масштаб l (наприклад, швидкість дисипації енергії e ~ b3 / l). Одним з найважливіших досягнень напівемпіричної теорії Т. є встановлення універсального (по числу Рейнольдса, при великих Re) логарифмічного закону для профілю швидкості в трубах, каналах і пограничному шарі: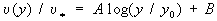 
,
справедливого на не дуже малих відстанях y від стінки; тут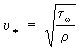 
(tw, - напруга тертя на стінці), А і В - постійні, а 
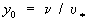, В разі гладкої стінки і пропорційно геометричній висоті горбків шорсткості в разі шорсткою.
Дрібномасштабні компоненти Т. (масштаби яких малі в порівнянні з масштабами течії в цілому) вносять істотний внесок в прискорення рідких частинок і в обумовлену ними здатність турбулентного потоку нести зважені частинки, в відносне розсіювання частинок і дроблення крапель в потоці, в перемішування турбулентних рідин, в генерацію магнітного поля в електропровідної рідини, в спектр неоднорідностей електронної щільності в іоносфері, в флуктуації параметрів електромагнітних хвиль, в бовтанку літальних апаратів і т.д.
Опис дрібномасштабних компонент Т. базується на гіпотезах Колмогорова, заснованих на уявленні про каскадному процесі передачі енергії від великомасштабних до все більш і більш дрібномасштабним компонентам Т. Внаслідок хаотичності і багатокаскадного цього процесу при дуже великих Re режим дрібномасштабних компонент виявляється просторово-однорідним, ізотропним і квазістаціонарним і визначається наявністю середнього припливу енергії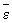 
від великомасштабних компонент і рівною йому середній дисипації енергії в області мінімальних масштабів. За першою гіпотезою Колмогорова, статистичні характеристики дрібномасштабних компонент визначаються лише двома параметрами: 
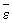і n; зокрема, мінімальний масштаб турбулентних неоднорідностей 
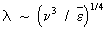(в атмосфері l ~ 10-1 см). За другою гіпотезою, при дуже великих Re в дрібномасштабної області існує такий (так званий інерційний) інтервал масштабів, великих в порівнянні з l, в якому параметр n виявляється неістотним, так що в цьому інтервалі характеристики Т. визначаються лише одним параметром 
.
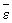Теорія подібності дрібномасштабних компонент Т. була використана для опису локальної структури полів температури, тиску, прискорення, пасивних домішок. Висновки теорії знайшли підтвердження при вимірах характеристик різних турбулентних течій. У 1962 А. Н. Колмогоров і А. М. Обухів запропонували уточнення теорії шляхом обліку флуктуацій поля дисипації енергії, статистичні властивості яких не універсальні: вони можуть бути різними в різних типах течій (і, зокрема, можуть залежати від Re).
Літ .: Монін А. С., Яглом А. М., Статистична гідромеханіки, ч. 1, М., 1965, ч. 2, М., 1967; Хінце І. О., Турбулентність, пров. з англ., М., 1963; Таунсенд А. А., Структура турбулентного потоку з поперечним зсувом, пров. з англ., М., 1959; Бетчелор Дж. К., Теорія однорідної турбулентності, пров. з англ., М., 1955; Ландау Л. Д., Ліфшиц Е. М., Механіка суцільних середовищ, 2 вид., М., 1954 (Теоретична фізика); Лінь Цзя-цзяо, Теорія гідродинамічної стійкості, пров. з англ., М., 1958; Лойцянський Л. Г., Механіка рідини і газу, 3 вид., М., 1970; Шлихтинг Г., Виникнення турбулентності, пров. з нім., М., 1962; Гідродинамічна нестійкість. Зб. статей, пров. з англ., М., 1964; Татарський В. І., Поширення хвиль в турбулентному атмосфері, М., 1967.
А. С. Монин.
