Теорема Декарта (геометрія)

1. Давніша історія [ правити | правити код ]

В геометрії теорема Декарта стверджує, що для будь-яких трьох взаємно стосуються кіл радіуси кіл задовольняють деякому квадратного рівняння . Вирішивши це рівняння, можна побудувати четверту окружність, що стосується інших трьох заданих кіл. Теорема названа на честь Рене Декарта , Який сформулював її в 1643 році.

Геометричні завдання на що стосуються окружності обговорювалися протягом тисячоліть. У стародавній Греції в III столітті до нашої ери Аполлоній Пергський присвятив цілу книгу цієї теми. На жаль, книга, яка носила назву Про торкання, не збереглася, загинувши при пожежі Олександрійської бібліотеки .

Рене Декарт обговорював завдання коротко в 1643 році в листі принцесі Єлизаветі Богемської . Він прийшов зовсім до того ж рішення, що наведено нижче в рівнянні (1), і тим самим вписав своє ім'я в теорему.

Фредерік Содді повторно відкрив рівняння в 1936 році. Стосуються окружності в цьому завданні іноді згадуються як Окружності Содді, можливо тому, що Содди вибрав публікацію своєї версії теореми у вигляді поеми під назвою The Kiss Precise (Акуратний поцілунок), який надруковано в журналі Nature (20 червня 1936). Содді узагальнив теорему на сфери. Торольд Госсет узагальнив теорему на довільні розмірності.

Давніша історія [ правити | правити код ]

Погляд Ігоря Шаригіна [1] : Протягом більшої частини періоду Едо (1603-1867) Японія перебувала майже в повній ізоляції від західного світу і розвивалася своїми шляхами, без впливу західних цивілізацій. Однак це не стало на заваді розвитку японської науки, зокрема математики. Особливо процвітала геометрія. Японці вважали, що мистецтво геометрії на те воля Божа. Нею захоплювалися представники всіх станів, від селян до самураїв. Свої відкриття, теореми вони зображували яскравими кольоровими фарбами на дошках - сангак - і вивішували при храмах - здебільшого синтоїстських, рідше буддистських - і усипальницях. Ці дошки були одночасно і його жертва шанованому божеству, і «публікацією» автора про зроблене їм красивому відкритті. Словесні пояснення майже відсутні. Автор як би говорив: «Дивись і, якщо зможеш, доведи!» ... Прекрасні завдання і теореми, зібрані в книзі «Японська храмова геометрія» - це своєрідне «обчислення кіл», «гімн окружності». Серед них знаходимо не тільки формулу Содді, але і її узагальнення на тривимірний випадок. Перша згадка про співвідношення між радіусами кіл з'явилося на дошці (сангак) в 1796 році в Токійській префектурі, повний доказ було опубліковано в 1830-м. Цікаво, що приклад, що показує зв'язок між радіусами п'яти дотичних сфер, був описаний на дошці, знайденої там же, а пізніше втраченої, вже в 1785 році. В середині XIX століття в Японії було опубліковано повний доказ «узагальненої формули для п'яти дотичних куль» ...

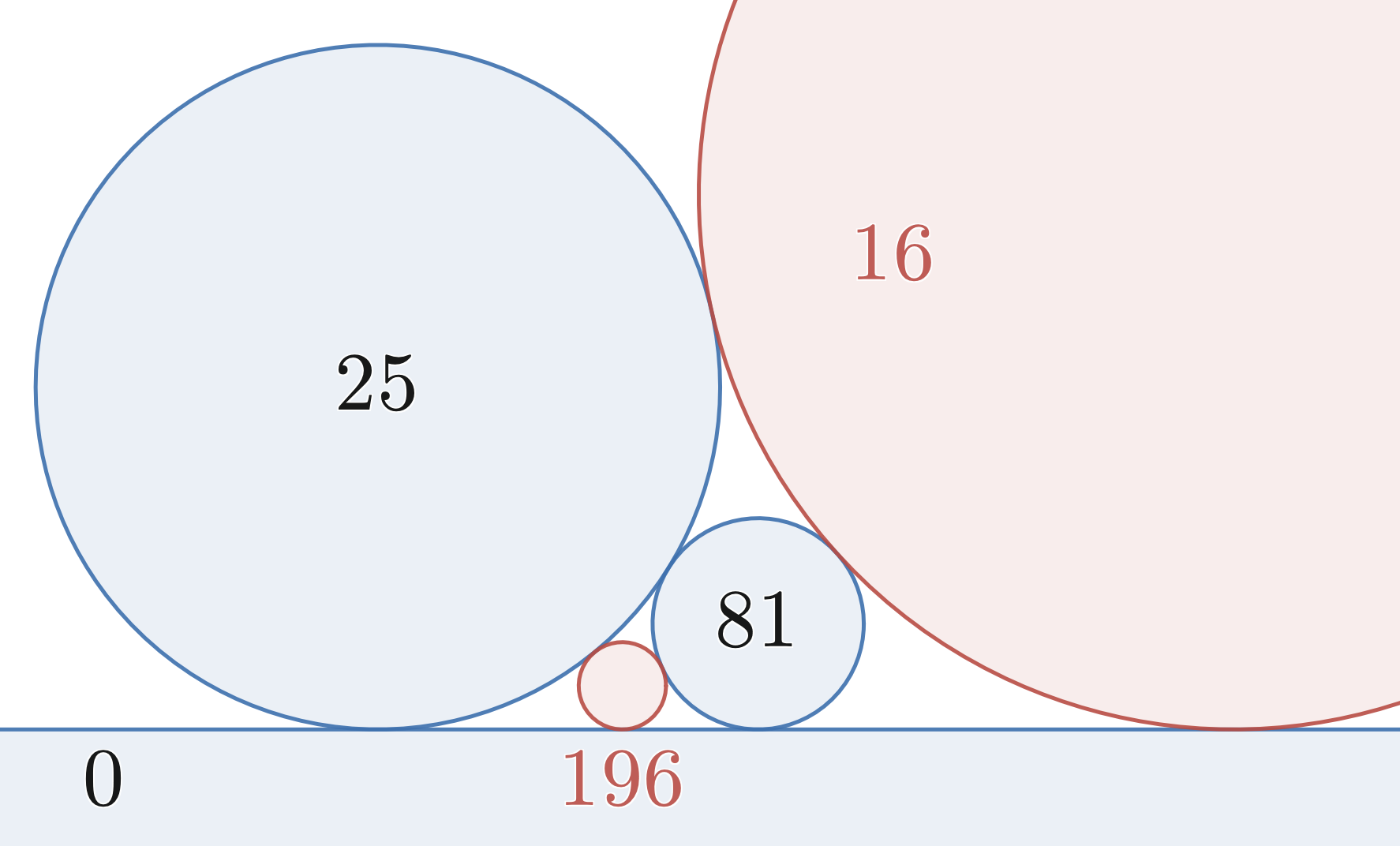
Теорему Декарта найпростіше сформулювати в термінах кривизни кіл. Кривизна кола визначається як k = ± 1 / r, де r - її радіус. Чим більше коло, тим менше величина її кривизни, і навпаки.

Знак плюс в k = ± 1 / r ставиться, якщо окружність має зовнішнє дотик до іншої окружності, як три чорних кола на малюнку. Для стосуються кіл внутрішньо, як велика червона окружність на малюнку, яка описує інші кола, ставиться знак мінус.

Якщо вважати, що пряма лінія - це вироджена окружність з нульовою кривизною (а отже, з нескінченним радіусом), теорема Декарта застосовна також і до прямої і двох кіл, що стосуються один одного попарно. В цьому випадку теорема дає радіус третьої окружності, що стосується двох інших і прямий.

Якщо чотири кола стосуються один одного в шести різних точках і окружності мають кривизни k i (для i = 1, ..., 4), теорема Декарта стверджує [2] :

(K 1 + k 2 + k 3 + k 4) 2 = 2 (k 1 2 + k 2 2 + k 3 2 + k 4 2). {\ Displaystyle (k_ {1} + k_ {2} + k_ {3} + k_ {4}) ^ {2} = 2 \, (k_ {1} ^ {2} + k_ {2} ^ {2} + k_ {3} ^ {2} + k_ {4} ^ {2}).} (1)

Якщо намагатися відшукати радіус четвертої окружності, що стосується трьох стосуються один одного кіл, рівняння краще записати у вигляді:

k 4 = k 1 + k 2 + k 3 ± 2 k 1 k 2 + k 2 k 3 + k 3 k 1. {\ Displaystyle k_ {4} = k_ {1} + k_ {2} + k_ {3} \ pm 2 {\ sqrt {k_ {1} k_ {2} + k_ {2} k_ {3} + k_ {3 } k_ {1}}}.} (2)

Знак ± відображає факт, що в загальному випадку є два рішення. Якщо виключити вироджений випадок прямої лінії, одне рішення позитивно, інше ж може бути як позитивним, так і негативним. Якщо рішення негативно, воно являє окружність, яка описує перших три (як показано на малюнку).

Одна з околиць замінена прямий (з нульовою кривизною). Теорема Декарта залишається вірною.

Якщо одну з околиць замінити на пряму лінію, то одне з чисел k i, скажімо, k 3, буде нульовим і випадає з рівняння (1). Рівняння (2) стає набагато простіше:

k 4 = k 1 + k 2 ± 2 k 1 k 2. {\ Displaystyle k_ {4} = k_ {1} + k_ {2} \ pm 2 {\ sqrt {k_ {1} k_ {2}}}.} (3)

Якщо дві окружності замінити прямими, дотик між двома колами замінюється паралельною двох прямих. Дві інші залишилися окружності повинні бути рівні. У цьому випадку, з k 2 = k 3 = 0, рівняння (2) стає тривіальним

k 4 = k 1. {\ Displaystyle \ displaystyle k_ {4} = k_ {1}.}

Неможливо замінити три кола прямими, оскільки одна окружність і три прямі не можуть торкатися один одного попарно. Теорема Декарта непридатна також до нагоди, коли всі чотири кола стосуються один одного в одній точці.

Ще один спеціальний випадок - коли ki є квадратами,

(V 2 + x 2 + y 2 + z 2) 2 = 2 (v 4 + x 4 + y 4 + z 4) {\ displaystyle (v ^ {2} + x ^ {2} + y ^ {2} + z ^ {2}) ^ {2} = 2 \, (v ^ {4} + x ^ {4} + y ^ {4} + z ^ {4})}

Ейлер показав, що еквівалентно трійці піфагорових трійок ,

(2 vx) 2 + (2 yz) 2 = (v 2 + x 2 - y 2 - z 2) 2 {\ displaystyle (2vx) ^ {2} + (2yz) ^ {2} = \, (v ^ {2} + x ^ {2} -y ^ {2} -z ^ {2}) ^ {2}} (2 vy) 2 + (2 xz) 2 = (v 2 - x 2 + y 2 - z 2) 2 {\ displaystyle (2vy) ^ {2} + (2xz) ^ {2} = \, (v ^ {2} -x ^ {2} + y ^ {2} -z ^ {2}) ^ {2}} (2 vz) 2 + (2 xy) 2 = (v 2 - x 2 - y 2 + z 2) 2 {\ displaystyle (2vz) ^ {2} + (2xy) ^ {2} = \, (v ^ {2} -x ^ {2} -y ^ {2} + z ^ {2}) ^ {2}}

і може бути задано параметричне представлення . Якщо вибрати негативний знак кривизни,

(- v 2 + x 2 + y 2 + z 2) 2 = 2 (v 4 + x 4 + y 4 + z 4) {\ displaystyle (-v ^ {2} + x ^ {2} + y ^ { 2} + z ^ {2}) ^ {2} = 2 \, (v ^ {4} + x ^ {4} + y ^ {4} + z ^ {4})}

рівняння можна представити у вигляді добре відомого параметричного рішення [3] ,

[V, x, y, z] = [2 (ab - cd) (ab + cd), (a 2 + b 2 + c 2 + d 2) (a 2 - b 2 + c 2 - d 2), 2 (ac - bd) (a 2 + c 2), 2 (ac - bd) (b 2 + d 2)] {\ displaystyle [v, x, y, z] = \, [2 (ab-cd) (ab + cd), (a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2}) (a ^ {2} -b ^ {2} + c ^ {2} - d ^ {2}), 2 (ac-bd) (a ^ {2} + c ^ {2}), 2 (ac-bd) (b ^ {2} + d ^ {2})]} ,

де

a 4 + b 4 = c 4 + d 4 {\ displaystyle a ^ {4} + b ^ {4} = \, c ^ {4} + d ^ {4}} .

Для визначення кола повністю потрібно знати не тільки її радіус (або кривизну), але потрібно ще знати і її центр. Відповідне рівняння найкраще написати, коли координати (x, y) представлені у вигляді комплексного числа z = x + i y. Рівняння тоді виглядає подібно до рівняння в теоремі Декарта і тому називається комплексної теоремою Декарта.

Якщо дані чотири кола з кривизнами k i і центрами z i (i = 1 ... 4), до того ж до рівності (1) виконується рівність:

(K 1 z 1 + k 2 z 2 + k 3 z 3 + k 4 z 4) 2 = 2 (k 1 2 z 1 2 + k 2 2 z 2 2 + k 3 2 z 3 2 + k 4 2 z 4 2). {\ Displaystyle (k_ {1} z_ {1} + k_ {2} z_ {2} + k_ {3} z_ {3} + k_ {4} z_ {4}) ^ {2} = 2 \, (k_ {1} ^ {2} z_ {1} ^ {2} + k_ {2} ^ {2} z_ {2} ^ {2} + k_ {3} ^ {2} z_ {3} ^ {2} + k_ {4} ^ {2} z_ {4} ^ {2}).} (4)

Після того, як k 4 буде знайдено за допомогою рівності (2), можна почати обчислення z 4 шляхом зміни рівняння (4) до виду, схожому на (2):

z 4 = z 1 k 1 + z 2 k 2 + z 3 k 3 ± 2 k 1 k 2 z 1 z 2 + k 2 k 3 z 2 z 3 + k 1 k 3 z 1 z 3 k 4. {\ Displaystyle z_ {4} = {\ frac {z_ {1} k_ {1} + z_ {2} k_ {2} + z_ {3} k_ {3} \ pm 2 {\ sqrt {k_ {1} k_ {2} z_ {1} z_ {2} + k_ {2} k_ {3} z_ {2} z_ {3} + k_ {1} k_ {3} z_ {1} z_ {3}}}} {k_ {4}}}.}

Знову, в загальному випадку, є два рішення для z 4, що відповідають двом рішенням для k 4.

Узагальнення для n-мірного простору іноді згадується як теорема Содді-Госсе, хоча це зроблено вже в 1886 Лахланом (R. Lachlan). В n-мірному евклідовому просторі максимальне число взаємно стосуються (N - 1) -мірних сфер одно n + 2. Наприклад, в 3-вимірному просторі можуть взаємно стосуватися п'ять сфер. Кривизни гіперсферу задовольняють рівняння

(Σ i = 1 n + 2 ki) 2 = n Σ i = 1 n + 2 ki 2 {\ displaystyle \ left (\ sum _ {i = 1} ^ {n + 2} k_ {i} \ right) ^ {2} = n \, \ sum _ {i = 1} ^ {n + 2} k_ {i} ^ {2}}

і випадок ki = 0 відповідає гиперплоскости, точно як в двовимірному випадку.

Хоча немає 3-мірних аналогів комплексним числам, зв'язок між місцями розташування центрів можна представити у вигляді матричних рівнянь [4] .