- розділ геометрії, в к-ром вивчаються властивості фігур, незмінні при конформних перетвореннях. Основним інваріантом К. г. є кут між напрямками.
К. р.- це геометрія , Певна в евклідовому просторі, доповненому однієї нескінченно віддаленої (невласне) точкою, з фундаментальної групою точкових перетворень, що переводять сфери в сфери Зазначене простір наз. конформних простором М п, а фундаментальна група - групою конформних Перетворюва н і й. У конформному просторі площину є сферою, що проходить через нескінченно віддалену точку
Наведене визначення К. р справедливо для простору будь-якого числа вимірів; в двовимірному випадку замість сфер говорять про колах (точніше кіл) При числі вимірювань 
перетворення, що переводять сфери в сфери, вичерпують всі перетворення, що зберігають кути ( теорема Ліувілля). При я = 2 група перетворень, що зберігають кути, ширше, однак і тут назва К. р зберігається за геометрією з фундаментальної групою точкових перетворень, що переводять кола на раду.
Будь-яке перетворення з фундаментальної групи К. р складається з кінцевого числа рухів, подібних перетворень і інверсій.
Фундаментальна група К. р площині М 2 ізоморфна деякої підгрупі проективної групи, саме підгрупі проектних перетворень тривимірного проективного простору Р3, що переводять в себе овальну поверхню 2-го порядку, т. Е. Групі гіперболічний. рухів тривимірного простору. Це дозволяє застосовувати для К. р зручний аналитич. апарат, к-рий використовується в неевклідових геометрії.
Будь-яка точка Р 3 визначається чотирма однорідними координатами х i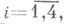 
або псевдовектори хс цими координатами. нехай
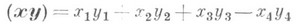- форма від векторів х, у; К овальна поверхня 2-го порядку Р 3, що задається рівнянням 
- 
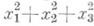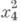= 0, або (XХ) = 0. Для точок поза К (xx)> 0, всередині - (хx). <0. За допомогою абсолюту Косуществляется стереографічна проекція точок абсолюту і точок поза абсолюту на конформну площину. Координати х, -,
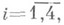точок Р 3 зв. тетрациклічними координатами точок і кіл на площині М 2. Так як при стереографіч. проекції точки на абсолюті переходять в точки на площині, а точки поза абсолюту - в кола на площині, то групі гіперболнч. рухів в Р 3 з абсолютом Кбудет відповідати група перетворень на площині, при яких точки переходять в точки, а кола - в кола, т. е. фундаментальна група К. р площині. Аналітично ця група задається формулами
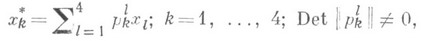
де M (х i) і М * (х * i) - точки до і після перетворень, причому форма
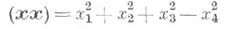
відрізняється від форми
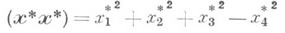
тільки множником. якщо ввести
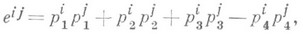
то умови збереження квадратичної форми запишуться у вигляді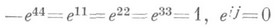 
при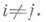 
При конформних перетвореннях невласна точка може переходити в будь-яку іншу точку, тому коло може перейти в пряму, і назад. Якщо зажадати, щоб невласна точка переходила в себе, т. Е. Щоб прямі переходили в прямі, то підгрупа таких перетворень є представником групи подібних перетворень (гомотетия і евклидово рух). У Р 3 підгрупі подібності відповідає підгрупа гтшерболпч. рухів, які залишають нерухомою недо-рую фіксовану точку абсолюту.
Іншим важливим класом конформних перетворень є інверсія. У Р 3 інверсії відповідає полярна гомология , Т. Е. Таке гіперболічний. рух , При к-ром кожна пара відповідних точок Мі М * лежить на прямій, що проходить через недо-рую фіксовану точку Свне абсолюту, і задовольняється умова: подвійне ставлення D (М, М *, С, N) = - 1. де N- точка перетину вказаною прямої з площиною, полярної точці Сотносітельно абсолюту. Також як будь-яке гнперболпч. рух можна отримати за допомогою кінцевого числа полярних гомології, так і будь-який конформне перетворення можна отримати за допомогою кінцевого числа інверсій.
Основним інваріантом К. р на площині є кут j між двома колами. Він виражається по-формулі
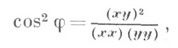
де x і у. - вектори, що відповідають двом колам з тетрацікліч. координатами х i і yi, -,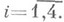 
У гіперболічний. геометрії Р 3 кут між колами на площині дорівнює неевклідову відстані між точками в просторі, відповідними колам. Инвариантность кута випливає з інваріантності відстані. Умова ортогональності Двох Кіл (xy) = 0, умова торкання (xx) (yy) - (xy) 2 = 0. Якщо один з кіл звертається в точку: (xx) = 0, то виходить умова инцидентности точки і кола (xy) - 0.
Найпростішим чином в М 2 є пучок кіл. Він задається рівнянням t = a p + b q, де р і q - фіксовані кола пучка. Залежно від знака D = (рр) (qq) - (pq) 2 пучки бувають: а) еліптичні (D> 0), б) гіперболічні (D <0), в) параболічні (D = 0) (див. Рис . 1).
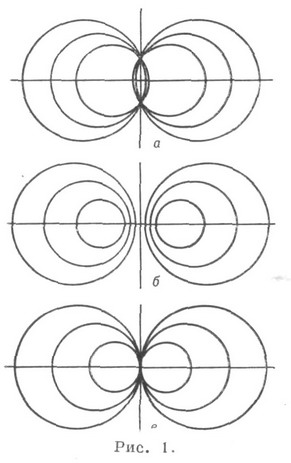
У Р 3 пучків кіл відповідають прямі. Еліптичному пучку - пряма , Не яка перетинає абсолют , Гіперболічному - пряма, яка перетинає абсолют, параболічного - пряма, яка стосується абсолюту. Так як у будь-якої прямої Р 3 є сполучена їй, то н у всякого пучка в М 2 є зв'язаний пучок.
Перетворення фундаментальної групи К. р площині це - перетворення, що задаються дрібно-лінійною функцією комплексного змінного.
У К. р тривимірного простору М 3 основними образами є точки н сфери. Задаються вони пентасферіческімі координатами xi,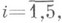 
або псевдовектори x. пятимерного простору. Кут між сферами визначається за тією ж формулою, що і кут між колами на площині.
Найпростіші образи в М 3: пучки сфер w = a y + b z, двупараметріч. зв'язки w = a x + b y + gzі трехпараметріч. зв'язки w = a x + b y + g z + dt сфер.
Коло в М 3 задається за допомогою елліптіч. пучка сфер, т. е. формулою
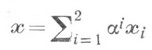
при додатковому умови
Кут q між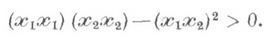 
кругом, заданим за допомогою сфер x 1, x2 і сферою у, визначається за формулою
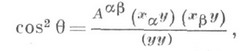
де Aab - алгебраїч. доповнення елементів визначника, складеного з А ab = x axb; . a, b = 1, 2. Пара кіл
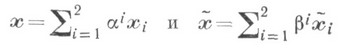
має два абсолютних інваріанта
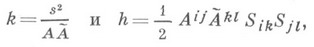
де
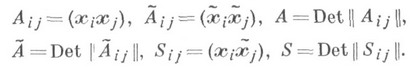
Для кожної пари кіл зі складових їх пучків можна виділити головні сфери. Це сфери, к-які задовольняють умовам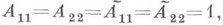 
A12 = = 0, S12-S21 = 0. Через ці сфери самі пучки задаються у вигляді
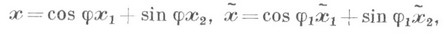
де j (j1) - кут між сферою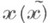 
і сферою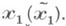 
Кути q1 і q2, під к-римі перетинаються головні сфери, першого кола з другим колом, наз. головними кутами пари кіл (вони збігаються з кутами, під к-римі головні сфери другого кола перетинаються з першим колом). Через головні кути інваріанти пари кіл виражаються наступним чином:
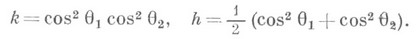
Головні кути q1 і q2 визначають екстремальні значення кутів, к-які сфери одного кола утворюють з іншим. Якщо q1 = q2, то для всіх сфер пари q = q1 = q2, п така пара кіл зв. ізогональной. За допомогою інваріантів пари кіл можна охарактеризувати
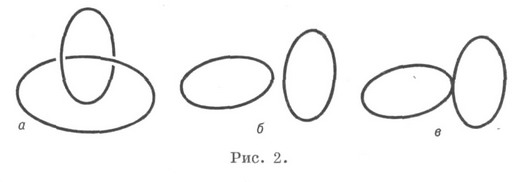
взаємне розташування двох кіл: а) зачеплені (i - 2h + k> 0), б) ізольовані (1-2 h + k <0), в) пересічні (1-2 h + k = 0), і умова лінійної незалежності сфер xi; і xi (див. рис. 2). Необхідна і достатня умова ізогональності пари кіл h2-k = 0. Використання в К. р методів математичного. аналізу привело до створення конформно-диференціальної геометрії. На основі К. р побудована геометрія простору конформной зв'язності, що відноситься до К. м як ріманова геометрія до евклідової. Для К. р на площині споживані також назви геометрія зворотних радіусів, кругова геометри я, інверсійна геометрія, а також геометрія Мебіуса (по імені А. Мебіуса, A. Mobius), вперше вивчав геометрію кругових перетворень.
Літ. : [1] Клейн Ф., Вища геометрія, пров. з нім., М.- Л., 1939; [2] Blaschke W., Vorlesungen uber Differential-Geometrie, Bd 3, В., 1929; [3] Бушманова Г. В., Норден А. II., Елементи конформной геометрії, Казань, 1972.
Г. В. Бушманова.
Математична енциклопедія. - М .: Радянська енциклопедія. І. М. Виноградов. 1977-1985.
