Теорія імовірності. Короткий курс для початківців

1. Рекомендований порядок вивчення теми:
2. Події. види подій
3. Спільні та несумісні події. Протилежні події. Повна група подій
4. алгебра подій
5. імовірність події
6. Класичне визначення ймовірності:

Мама мила раму

Під завісу тривалих літніх канікул настав час потихеньку повертатися до вищої математики та урочисто відкрити порожній вёрдовскій файл, щоб приступити до створення нового розділу - Теорія ймовірностей і математична статистика. Зізнаюся, нелегко даються перші рядки, але перший крок - це півшляху, тому я пропоную всім уважно простудіювати вступну статтю, після чого освоювати тему буде в 2 рази простіше! Нітрохи не перебільшую. ... Напередодні чергового 1 вересня згадується перший клас і буквар .... Букви складаються в склади, склади в слова, слова в короткі речення - Мама мила раму. Справитися з тервером і математичною статистикою так само просто, як навчитися читати! Однак для цього необхідно знати ключові терміни, поняття і позначення, а також деякі специфічні правила, яким і присвячений даний урок.

Але спочатку прийміть мої вітання з початком (продовженням, завершенням, потрібне відзначити) навчального року і прийміть подарунок. Кращий подарунок - це книга, і для самостійної роботи я рекомендую наступну літературу:

1) Гмурман В.Є. Теорія ймовірностей і математична статистика

Легендарне навчальний посібник, що витримало більше десяти перевидань. Відрізняється дохідливістю і граничної простий викладу матеріалу, а перші розділи так і зовсім доступні, думаю, вже для учнів 6-7-х класів.

2) Гмурман В.Є. Керівництво вирішення задач з теорії ймовірностей і математичній статистиці

Решебник того ж Володимира Юхимовича з детально розібраними прикладами і завданнями.

ОБОВ'ЯЗКОВО закачайте обидві книги з Інтернету або роздобудьте їх паперові оригінали! Підійде і версія 60-70-х років, що навіть краще для чайників. Хоча фраза «теорія ймовірностей для чайників» звучить досить безглуздо, оскільки майже все обмежується елементарними арифметичними діями. Проскакують, правда, місцями похідні і інтеграли , Але це тільки місцями.

Я постараюся досягти тієї ж ясності викладу, але повинен попередити, що мій курс орієнтований на вирішення завдань і теоретичні викладки зведені до мінімуму. Таким чином, якщо вам потрібна розгорнута теорія, доведення теорем (теорем-теорем!), Будь ласка, зверніться до підручника. Ну, а хто хоче навчитися вирішувати завдання з теорії ймовірностей і математичній статистиці в найкоротші терміни, йдіть за мною!

Рекомендований порядок вивчення теми:

Ця стаття;
Завдання з комбінаторики. приклади рішень ;
Завдання на класичне визначення ймовірності ;
Геометричне визначення ймовірності ;
Теореми додавання та множення ймовірностей ;
Зовсім події ;
Формула повної ймовірності та формули Байєса ;
Незалежні випробування і формула Бернуллі ;
Локальна і інтегральна теореми Лапласа ;
Статистичне визначення ймовірності .

Для початку вистачить =)

У міру прочитання статей доцільно знайомитися (хоча б побіжно) з додатковими завданнями розглянутих видів. На сторінці Готові рішення з вищої математики розміщуватимуться відповідні pdf-ки з прикладами рішень. Також значну допомогу нададуть ІДЗ 18.1 Рябушко (Простіше) і прорешать ІДЗ за збірником чудесенка (Складніше).

Крім того, на складі математичних формул і таблиць корисно відкрити / закачати / роздрукувати допоміжні довідкові файли - Основні формули комбінаторики і Основні формули теорії ймовірностей ..

Отже, дорожні покажчики розставлені, і ми починаємо шлях з теорії ймовірностей, яку неодноразово просили висвітлити відвідувачі сайту.

Перше і дуже важливе. Що вивчає ця наука? Багатьом в голову напевно прийшли думки на кшталт «ймовірність дощу велика», «ймовірність виграшу в лотерею мала», «орел і решка випадають з імовірністю 50 на 50» і т.п. Але тоді відразу виникає питання, при чому тут наука? Будь ласка, прямо зараз візьміть в руки монету і скажіть, який гранню вона випаде після кидка? ... Зовсім не схоже на теорію - скоріше якесь ворожіння ....

І дійсно, обивательське розуміння ймовірності більше скидається на якесь пророкування, часто з неабиякою часткою містицизму і забобонів. Теорія ж ймовірностей вивчає імовірнісні закономірності масових однорідних випадкових подій. Тобто, у неї немає мети щось вгадати, наприклад, результат кидка тієї ж монети в одиничному експерименті. Однак якщо одну і ту ж монету в однакових умовах підкидати сотні і тисячі разів, то буде простежуватися чітка закономірність, описувана цілком жорсткими законами.

Інший приклад. Навколо кожного з нас літають молекули повітря. Деякі з них мають високу, деякі середньої, а деякі - низькою швидкістю. Не має сенсу вгадувати швидкість окремо взятих молекул; але їх масовий облік знаходить найширше застосування в теоретичних і прикладних фізичних дослідженнях. Зверніть увагу, що літаки «вміють» літати, газові та парові котли зазвичай не вибухають, а чайники при кипінні не стрибають по кухні. За багатьма і багатьма, здавалося б, повсякденними фактами і подіями криються серйозні ймовірносно-статистичні розрахунки.

Або приклад простіше. Якщо ви придбаєте лотерейний квиток, то навряд чи щось виграєте і зовсім неймовірно, що зірвете великий куш. Але організатор лотереї навіть при випадковому розіграші тиражу (витяг пронумерованих кульок і т.п. або якщо учасники самі вгадують номера) гарантовано і з високою точністю знає, скільки квитків виграють / програють, і, зрозуміло, залишається в прибутку. Лотереї часто називають обманом, однак парадокс полягає в тому, що ця гарантія строго обгрунтована теорією; рівних, як і життєва фраза «все одно нічого не виграю». Думаю, тепер все зрозуміли правильний спосіб заробітку на лотереях =) Втім, ми ще повернемося до «секретів» виграшу в рулетку і різні лотереї.

Так, до речі подумайте ще над однією нагальною завданням: багато хто з нас за життя здають десятки іспитів, і практично завжди має місце наступна ситуація: частина питань студент знає (або заготовлені шпори), а частина питань - не знає (або плаває як майстер спорту) . Настає день «X»: ранок, коридор з 10-15 однокурсниками і двері, за якої на столі лежить повний комплект квитків. В якому випадку найімовірніше скласти іспит - якщо йти «в перших рядах», «в серединці» або якщо зайти в аудиторію в числі останніх? ... Вивчаємо теорію ймовірностей!

Спочатку розбираємося з основними термінами, які нижче по тексту я буду виділяти жирним курсивом. Звертаю вашу увагу, що це САМЕ ТЕРМІНИ, а не «просто слова»!

Події. види подій

Одне з базових понять тервера вже озвучено вище - це подія. Події бувають достовірними, неможливими і випадковими.

Вірогідним називають подія, яке в результаті випробування (здійснення певних дій, певного комплексу умов) обов'язково відбудеться. Наприклад, в умовах земного тяжіння підкинута монета неодмінно впаде вниз.

Неможливим називають подія, яке явно не відбудеться в результаті випробування. Приклад неможливого події: в умовах земного тяжіння підкинута монета полетить вгору.

І, нарешті, подія називається випадковим, якщо в результаті випробування воно може, як статися, так і не відбутися, при цьому повинен мати місце принциповий критерій випадковості: випадкова подія - є наслідок випадкових факторів, вплив яких передбачити неможливо або вкрай важко. Приклад: в результаті кидка монети випаде «орел». У розглянутому випадку випадкові чинники - це форма і фізичні характеристики монети, сила / напрямок кидка, опір повітря і т.д.

Підкреслений критерій удачі є дуже важливим - так, наприклад, картковий шулер може дуже спритно імітувати випадковість і давати вигравати жертві, але ні про які випадкових факторах, що впливають на підсумковий результат, мови не йде.

Будь-який результат випробування називається результатом, який, власне і є поява певної події. Зокрема, при підкиданні монети можливо 2 результату (випадкових події): випаде орел, випаде решка. Природно, мається на увазі, що дане випробування проводиться в таких умовах, що монета не може встати на ребро або, скажімо, зависнути в невагомості.

Події (будь-які) позначають великими латинськими літерами 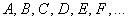або тими ж буквами з підрядковими індексами, наприклад: 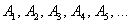. Винятком є ​​літера 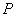, Яка зарезервована під інші потреби.

Запишемо наступні випадкові події:

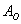- в результаті кидка монети випаде «орел»;
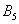- в результаті кидка гральної кістки (кубика) випаде 5 очок;
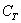- з колоди буде залучена карта трефової масті (за замовчуванням колода вважається повною).

Так, події прямо так і записують в практичних завданнях, при цьому в доречних випадках зручно використовувати «говорять» підрядкові індекси (хоча можна обійтися і без них).

Слід в третій раз підкреслити, що випадкові події обов'язково задовольняють вищенаведені критерієм випадковості. У цьому сенсі знову показовий 3-й приклад: якщо з колоди спочатку видалити всі карти трефової масті, то подія 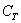стає неможливим. Навпаки, якщо випробувачеві відомо, що, наприклад, дама треф лежить знизу, то він при бажанні може зробити подію 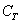достовірним =) Таким чином, в даному прикладі передбачається, що карти добре перемішані і їх сорочки невиразні, тобто колода не є крапчастою. Причому, тут під «крапом» розуміються навіть не «умілі руки», які ліквідують випадковість вашого виграшу, а видимі дефекти карт. Наприклад, сорочка тієї ж пані треф може бути брудною, порваній, заклеєною скотчем ... блін, якийсь посібник для початківця Чикатило вийшло =)

Таким чином, при розіграші важливого жереба завжди є сенс ненароком подивитися, а не однакові чи межі монети ;-)

Інша важлива характеристика подій - це їх рівно можливих. Два або більша кількість подій називають рівноможливими, якщо жодна з них не є більш можливим, ніж інші. наприклад:

випадання орла чи решки при кидку монети;
випадання 1, 2, 3, 4, 5 або 6 очок при кидку грального кубика;
виймання картки трефової, пікової, бубновою або Червової масті з колоди.

При цьому передбачається, що монета і кубик однорідні і мають геометрично правильну форму, а колода добре перемішана і «ідеальна» з точки зору нерозрізненості сорочок карт.

Чи можуть бути ті ж події не рівно можливими? Можуть! Наприклад, якщо у монети або кубика зміщений центр ваги , То набагато частіше будуть випадати цілком певні межі. Як то кажуть, ще одна лазівка ​​для шахраїв. події 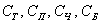- витяг трефи, піки, черви або бубни теж рівноможливими. Однак рівно можливих легко порушить фокусник, який, тасуючи колоду (навіть «ідеальну»), спритно підгляне і сховає в рукаві, наприклад, туза треф. Тут стає менш можливим, що опонентові буде здана трефа, і, головне, менш можливо, що буде зданий туз.

Проте, в розглянутих трьох випадках при втраті рівно можливих все ж зберігається випадковість подій.

Спільні та несумісні події. Протилежні події.
Повна група подій

Події називають несумісними, якщо в одному і тому ж випробуванні поява однієї з подій виключає появу інших подій. Найпростішим прикладом несумісних подій є пара протилежних подій. Подія, протилежне даному, звичайно позначається тією ж латинською літерою з рискою вгорі. наприклад:

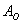- в результаті кидка монети випаде орел;
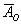- в результаті кидка монети випаде решка.

Цілком зрозуміло, що в окремо взятому випробуванні поява орла виключає появу решки (і навпаки), тому дані події і називаються несумісними.

Протилежні події легко формулюються з міркувань елементарної логіки:

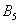- в результаті кидка грального кубика випаде 5 очок;
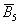- в результаті кидка грального кубика випаде число очок, відмінне від п'яти.

Або п'ять, або не п'ять - третього не дано, тобто події несумісні і протилежні.

Аналогічно - або трефа або карта іншої масті:

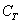- з колоди буде залучена карта трефової мира,
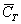- з колоди буде залучена піку, черва або бубна.

Безліч несумісних подій утворюють повну групу подій, якщо в результаті окремо взятого випробування обов'язково з'явиться одне з цих подій. Очевидно, що будь-яка пара протилежних подій (зокрема, приклади вище) утворює повну групу. Однак в різних завданнях з одним і тим же об'єктом можуть фігурувати різні події, наприклад, для грального кубика характерно розгляд наступного набору:

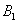- в результаті кидка грального кубика випаде 1 очко;
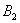- ... 2 очка;
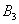- ... 3 очка;
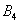- ... 4 очка;
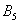- ... 5 очок;
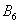- ... 6 очок.

події 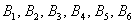несумісні (оскільки поява будь-якої межі виключає одночасна поява інших) і утворюють повну групу (так як в результаті випробування неодмінно з'явиться одне з цих шести подій).

Ще одне важливе поняття, яке нам скоро буде потрібно - це елементарність результату (події). Якщо зовсім просто, то елементарна подія «не можна розкласти на інші події». Наприклад, події 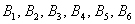елементарні, але подія 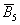не є таким, оскільки передбачає випадання 1, 2, 3, 4 або 6 очок (включає в себе 5 елементарних фіналів).

У прикладі з картами події 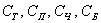(Витяг трефи, піки, черви або бубни відповідно) несумісні і утворюють повну групу, але вони Неелементарні. Якщо вважати, що в колоді 36 карт, то кожен із перелічених подій включає в себе 9 елементарних фіналів. Аналогічно - події 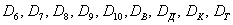(Витяг шістки, сімки, ..., короля, туза) несумісні, утворюють повну групу і Неелементарні (кожне включає в себе 4 випадки).

Таким чином, елементарним результатом тут вважається лише витяг якоїсь конкретної карти, і, зрозуміло, 36 несумісних елементарних фіналів теж утворюють повну групу подій.

Спільні події менш значимі з точки зору вирішення практичних завдань, але обходити їх стороною не будемо. Події називаються спільними, якщо в окремо взятому випробуванні поява одного з них не виключає появу іншого. наприклад:

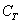- з колоди карт буде залучена трефа;
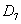- з колоди карт буде залучена сімка.

Якщо бути зовсім лаконічним, одне не виключає іншого.

Поняття спільності охоплює і більша кількість подій:

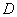- завтра о 12.00 буде дощ;
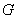- завтра о 12.00 буде гроза;
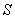- завтра о 12.00 буде сонце.

Ситуація, звичайно, досить рідкісна, але спільне поява всіх трьох подій в принципі не виключено. Слід зазначити, що перераховані події сумісні і попарно, тобто може бути тільки злива з грозою або грибний дощик, або погромихает неподалік на тлі ясного неба.

алгебра подій

Тримайтеся, буде і матан =)

Будь ласка, запам'ятайте НАЙВАЖЛИВІШИЙ ПРАВИЛО, без якого освоїти тервер просто нереально:

Операція складання подій означає логічний зв'язку АБО,
а операція множення подій - логічний зв'язку І.

1) Сумою двох подій 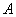і 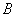називається подія 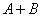яке полягає в тому, що настане або подія 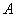або подія 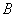або обидві події одночасно. У тому випадку, якщо події несумісні, останній варіант відпадає, тобто може наступити або подія 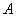або подія .

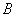Правило поширюється і на більша кількість доданків, наприклад, подія 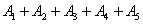полягає в тому, що станеться хоча б одна з подій 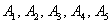, А якщо події несумісні - то одне і тільки одна подія з цієї суми: або подія 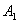, Або подія 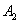, Або подія 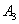, Або подія 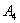, Або подія .

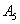Прикладів маса:

події 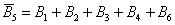(при кидку гральної кістки не випаде 5 очок) полягає в тому, що випаде або 1, або 2, або 3, або 4, або 6 очок.

подія 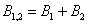(випаде не більше двох очок) полягає в тому, що з'явиться 1 або 2 очка.

подія 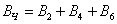(буде парне число очок) полягає в тому, що випаде або 2 або 4 або 6 очок.

подія 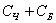полягає в тому, що з колоди буде залучена карта червоної масті (чирва або бубна), а подія 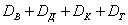- в тому, що буде залучена «картинка» (валет чи дама або король або туз).

Трохи цікавіше справа з спільними подіями:

подія 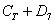полягає в тому, що з колоди буде залучена трефа або сімка або сімка треф. Відповідно до даного вище визначення, хоча б щось - або будь-яка трефа або будь-яка сімка або їх «перетин» - сімка треф. Легко підрахувати, що цієї події відповідає 12 елементарних фіналів (9 трефових карт + 3 залишилися сімки).

подія 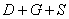полягає в тому, що завтра о 12.00 настане ХОЧА Б ОДИН з сумміруемих спільних подій, а саме:

- або буде тільки дощ / тільки гроза / тільки сонце;
- або настане тільки якась пара подій (дощ + гроза / дощ + сонце / гроза + сонце);
- або всі три події з'являться одночасно.

Тобто, подія 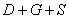включає в себе 7 можливих результатів.

Другий стовп алгебри подій:

2) творити двох поді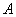й и 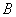назівають подію 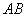, Яке складається в спільному появу цих подій, іншими словами, множення 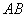означає, що при деяких обставинах настане і подія 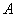, І подія 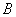. Аналогічне твердження справедливе і для більшого кількості подій, так, наприклад, твір 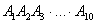має на увазі, що при певних умовах відбудеться і подія 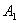, І подія 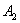, І подія 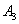, ..., і подія .

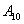Розглянемо випробування, в якому підкидаються дві монетиі наступні події:

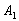- на 1-й монеті випаде орел;
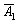- на 1-й монеті випаде решка;
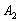- на 2-й монеті випаде орел;
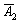- на 2-й монеті випаде решка.

тоді:
- подія 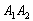полягає в тому, що на обох монетах (на 1-й і на 2-й) випаде орел;
- подія 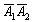полягає в тому, що на обох монетах (на 1-й і на 2-й) випаде решка;
- подія 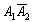полягає в тому, що на 1-й монеті випаде орел і на 2-й монеті решка;
- подія 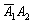полягає в тому, що на 1-й монеті випаде решка і на 2-й монеті орел.

Неважко помітити, що події 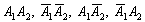несумісні (тому що не може, наприклад, випасти 2 орла і в той же самий час 2 решки) і утворюють повну групу (оскільки враховані всі можливі результати кидка двох монет). Давайте підсумуємо дані події: 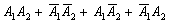. Як інтерпретувати цю запис? Дуже просто - множення означає логічний зв'язку І, а додавання - АБО. Таким чином, суму 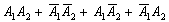легко прочитати зрозумілим людською мовою: «випадуть два орла або дві решки або на 1-й монеті випаде орел і на 2-й решка або на 1-й монеті випаде решка і на 2-й монеті орел»

Це був приклад, коли в одному випробуванні задіяно кілька об'єктів, в даному випадку - дві монети. Інша поширена в практичних завданнях схема - це повторні випробування, коли, наприклад, один і той же гральний кубик кидається 3 рази поспіль. В якості демонстрації розглянемо наступні події: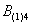
- в 1-му кидку випаде 4 очка;
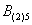- у 2-му кидку випаде 5 очок;
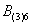- в 3-м кидку випаде 6 очок.

тоді подія 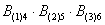полягає в тому, що в 1-му кидку випаде 4 очка і в 2-му кидку випаде 5 очок і в 3-му кидку випаде 6 очок. Очевидно, що у випадку з кубиком буде значно більше комбінацій (Результатів), ніж, якби ми підкидали монету.

... Розумію, що, можливо, розбираються не надто цікаві приклади, але це часто зустрічаються в задачах речі і від них нікуди не дітися. Крім монетки, кубика і колоди карт вас чекають урни з різнокольоровими кульками, кілька анонімів, що стріляють по мішені, і невтомний робочий, який постійно виточує якісь деталі =)

імовірність події

Імовірність події - це центральне поняття теорії ймовірностей. ... Убивчо логічна річ, але з чогось треба було починати =) Існує кілька підходів до її визначення:

Класичне визначення ймовірності;
Геометричне визначення ймовірності ;
Статистичне визначення ймовірності .

У даній статті я зупинюся на класичному визначенні ймовірностей, яке знаходить найбільш широке застосування в навчальних завданнях.

Позначення. Імовірність деякої події 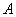позначається великою латинською літерою 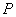, А сама подія береться в дужки, виступаючи в ролі своєрідного аргументу. например:

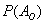- ймовірність того, що в результаті кидка монети випаде «орел»;
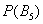- ймовірність того, що в результаті кидка гральної кістки випаде 5 очок;
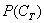- ймовірність того, що з колоди буде залучена карта трефової масті.

Також для позначення ймовірності широко використовується маленька буква 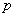. Зокрема, можна відмовитися від громіздких позначень подій 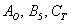і їх ймовірностей 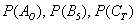на користь наступної стилістики ::

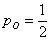- ймовірність того, що в результаті кидка монети випаде «орел»;
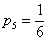- ймовірність того, що в результаті кидка гральної кістки випаде 5 очок;
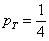- ймовірність того, що з колоди буде залучена карта трефової масті.

Даний варіант популярний при вирішенні практичних завдань, оскільки дозволяє помітно скоротити запис рішення. Як і в першому випадку, тут зручно використовувати «говорять» підрядкові / надрядкові індекси.

Всі вже давно здогадалися про числах, які я тільки що записав вище, і зараз ми дізнаємося, як вони вийшли:

Класичне визначення ймовірності:

Ймовірністю настання події 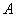в деякому випробуванні називають відношення 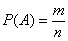, Де:

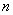- загальне число всіх рівно можливих, елементарних фіналів цього випробування, які утворюють повну групу подій;

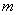- кількість елементарних фіналів, що сприяють події .

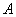При кидку монети може випасти або орел, або решка - дані події утворюють повну групу, таким чином, загальне число випадків 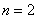; при цьому, кожен з них елементарний і равновозможен. події 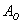сприяє 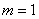результат (випадання орла). За класичним визначенням ймовірностей: .

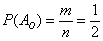Аналогічно - в результаті кидка кубика може з'явитися 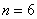елементарних рівно можливих випадків, що утворюють повну групу, а події 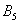сприяє єдиний 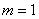результат (випадання п'ятірки). тому: .

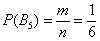Особливу увагу звертаю на третій приклад. Тут буде некоректним сказати «раз в колоді 4 масті, то ймовірність отримання трефи 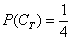». У визначенні мова йде про елементарні випадки, тому правильний порядок міркувань такий: всього в колоді 36 карт (несумісні елементарні результати, що утворюють повну групу), з них 9 карт трефової масті (к-ть елементарних фіналів, що сприяють події 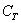); за класичним визначенням ймовірності: 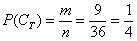. Саме так!

Ймовірності можна висловити і в процентах, наприклад: ймовірність випадання орла дорівнює 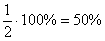, Випадання п'ятірки 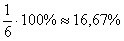, Вилучення трефи 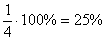, Але в теорії ймовірностей ЦЬОГО РОБИТИ НЕ ПРИЙНЯТО (хоча не забороняється прикидати відсотки в умі).

Прийнято використовувати частки одиниці, і, очевидно, що ймовірність може змінюватися в межах 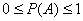. При цьом если 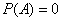, То подія 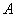є неможливим, якщо 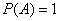- достовірним, а якщо 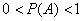, То мова йде про випадковий подію.

! Якщо в ході рішення будь-якої задачі у вас вийшло якесь інше значення ймовірності - шукайте помилку!

При класичному підході до визначення ймовірності крайні значення (нуль і одиниця) виходять за допомогою точно таких же міркувань. Нехай з якоїсь урни, в якій знаходяться 10 червоних куль, навмання витягується 1 куля. Розглянемо наступні події:

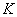- з урни буде витягнуто червоний куля;
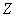- з урни буде витягнуто зелений куля.

Загальна кількість випадків: 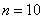. події 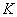сприяють всі можливі наслідки 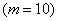, Отже, 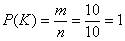, Тобто дана подія достовірно. Для 2-го ж події сприяють результати відсутні 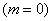, тому 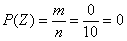, Тобто подія 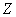неможливо.

Особливий інтерес представляють події, ймовірність настання яких надзвичайно мала. Хоч такі події і є випадковими, для них справедливий наступний постулат:

в одиничному випробуванні малоймовірно подія не відбудеться.

Саме, тому Ви не зірвете в лотереї Джек-пот, якщо ймовірність цієї події, скажімо, дорівнює 0,00000001. Так-так, саме Ви - з єдиним квитком в якомусь конкретному тиражі. Втім, більша кількість квитків і більша кількість розіграшів Вам особливо не допоможуть. ... Коли я розповідаю про це оточуючим, то майже завжди у відповідь чую: «але ж хтось виграє». Добре, тоді давайте проведемо наступний експеримент: будь ласка, сьогодні або завтра купите квиток будь-лотереї (не відкладайте!). І якщо виграєте ... ну, хоча б більше 10 кілорублей, обов'язково відпишіться - я поясню, чому це сталося. За відсоток, зрозуміло =) =)

Але сумувати не потрібно, тому що є протилежний принцип: якщо ймовірність деякої події дуже близька до одиниці, то в окремо взятому випробуванні воно практично достовірно відбудеться. Тому перед стрибком з парашутом не треба боятися, навпаки - посміхайтеся! Адже повинні скластися зовсім немислимі і фантастичні обставини, щоб відмовили обидва парашута.

Хоча все це лірика, оскільки в залежності від вмісту події перший принцип може виявитися веселим, а другий - сумним; або взагалі обидва паралельними.

Мабуть, поки достатньо, на уроці Завдання на класичне визначення ймовірності ми вичавимо максимум з формули 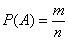. У заключній же частині цієї статті розглянемо одну важливу теорему:

Сума ймовірностей подій, які утворюють повну групу, дорівнює одиниці. Грубо кажучи, якщо події утворюють повну групу, то зі 100% -й вірогідністю якесь із них відбудеться. У найпростішому випадку повну групу утворюють протилежні події, наприклад:

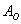- в результаті кидка монети випаде орел;
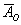- в результаті кидка монети випаде решка.

По теоремі: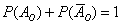

Цілком зрозуміло, що дані події рівноможливими і їх ймовірності однакові .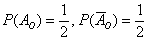

Унаслідок рівності ймовірностей рівноможливими події часто називають рівноімовірними. А ось і скоромовка на визначення ступеня сп'яніння вийшла =)

Приклад з кубиком: події 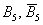протилежні, тому .

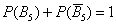Вже згадана теорема зручна тим, що дозволяє швидко знайти ймовірність протилежної події. Так, якщо відома ймовірність 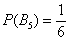того, що випаде п'ятірка, легко обчислити вірогідність того, що вона не випаде:

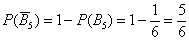
Це набагато простіше, ніж підсумувати ймовірності п'яти елементарних фіналів. Для елементарних фіналів, до речі, дана теорема теж справедлива: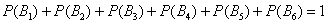

події 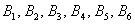, Як зазначалося вище, рівноможливими - і тепер ми можемо сказати, що різновірогідні. Вірогідність випадання будь-якої грані кубика дорівнює :

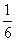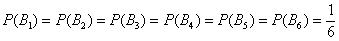
Ну і на закуску колода: оскільки нам відома ймовірність 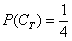того, що буде залучена трефа, то легко знайти ймовірність того, що буде залучена карта іншої масті: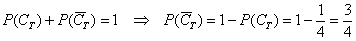

Зауважте, що розглянуті пари поді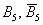й и 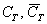НЕ рівноймовірно, як воно найчастіше і буває.

У спрощеній версії запису рішення ймовірність протилежної події стандартно позначається рядкової буквою 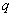. Например, если 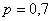- ймовірність того, що стрілець потрапить в ціль, то 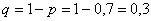- ймовірність того, що він промахнеться.

! У теорії ймовірностей літер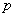и и 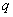небажано використовувати в якихось інших цілях.

На честь Дня Знань я не буду задавати домашнє завдання =), але дуже важливо, щоб ви могли відповісти на наступні питання:

- Які види подій існують?
- Що таке випадковість і рівно можливих події?
- Як ви розумієте терміни спільність / несумісних подій?
- Що таке повна група подій, протилежні події?
- Що означає додавання і множення подій?
- У чому суть класичного визначення ймовірності?
- Чим корисна теорема додавання ймовірностей подій, що утворюють повну групу?

Ні, зубрити нічого не треба, це всього лише ази теорії ймовірностей - своєрідний буквар, який досить швидко вкладеться в голові. І щоб це сталося якомога швидше, пропоную ознайомитися з уроками Завдання з комбінаторики и Завдання на класичне визначення ймовірності .

Успіхів!

Автор: Ємелін Олександр

Вища математика для заочніків і не тільки >>>

(Перехід на головну сторінку)